Chapter 7: Graph Algorithms
Section 7.1 Directed Graphs and Binary Relations
Next we discuss a more efficient algorithm for computing the transitive closure of a relation (or the reachability matrix of a graph).
Warshall's Algorithm is an algorithm used to compute the transitive closure of a directed graph. The transitive closure of a graph tells you which vertices (nodes) are reachable from which other vertices, meaning if there is a path between two vertices, either directly or through other vertices. The algorithm is particularly useful in determining reachability in graphs.
Warshall's Algorithm

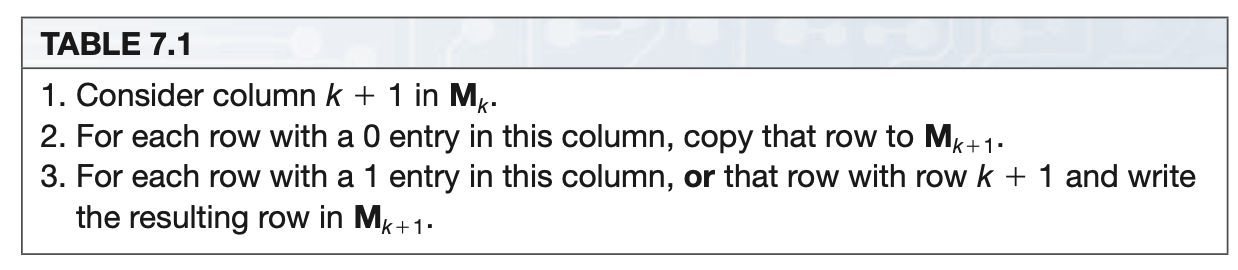
Table 7.1 describes the (informal) steps to compute entries in \(M_{k+1}\) from matrix \(M_k\).
Example



Practice
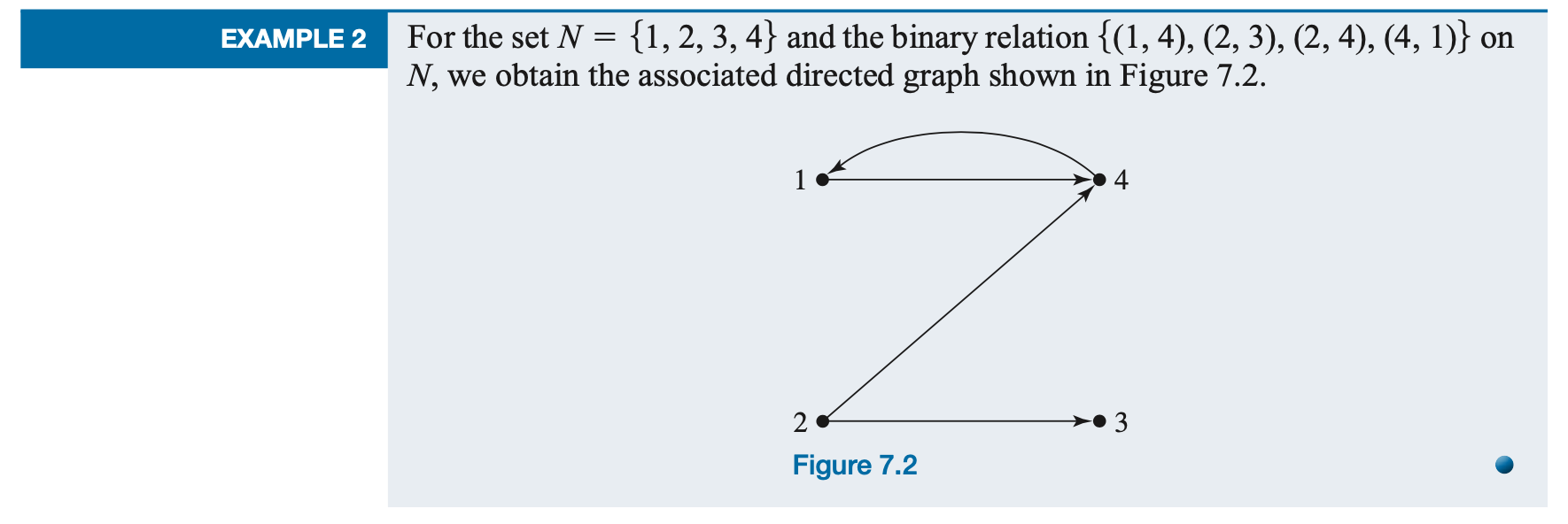
Please use Warshall's algorithm to compute reachability matrix R for the graph of Figure 7.2.