Chapter 9: Finite-State Machines, Turing machines
Section 9.4 Turing Machines
Turing Machines
To simulate more general computational procedures than the finite-state machine can handle, we use a Turing machine , proposed by the British mathematician Alan M. Turing in 1936. Turing machine is essentially a finite-state machine with the added ability to reread its input and also to erase and write over its input. It also has unlimited auxiliary memory. Thus, the Turing machine overcomes the deficiencies we noted in finite-state machines. Unlimited auxiliary memory makes the Turing machine a hypothetical "machine" -- a model--not a real device.
A Turing machine is an abstract computational model that performs computations by reading and writing to an infinite tape. Turing machines are similar to finite automata/finite state machines but have the advantage of unlimited memory. They are capable of simulating common computers; a problem that a common computer can solve (given enough memory) will also be solvable using a Turing machine, and vice versa. Turing machines were invented by the esteemed computer scientist Alan Turing in 1936. It is a simple yet powerful abstract machine that serves as a fundamental concept in the field of theoretical computer science.
The Turing machine was designed to explore the limits of what is computable.
Simulating a Computer: A Turing machine can simulate any algorithm that runs on a modern computer. If a problem can be solved on a common computer (such as finding the solution to a mathematical equation or running a program), a Turing machine can also solve it, provided it has sufficient memory and time.
Limitations: Both Turing machines and modern computers share certain limitations. There are problems that are undecidable (such as the Halting Problem) that neither a Turing machine nor any other computer can solve algorithmically for all possible inputs.
Turing Machine
A Turing machine consists of a finite-state machine and an unlimited tape divided into cells, each cell containing at most one symbol from an allowable finite alphabet. At any one instant, only a finite number of cells on the tape are nonblank. We use the special symbol b to denote a blank cell. The finite-state unit, through its read-write head, reads one cell of the tape at any given moment (Figure 9.15).
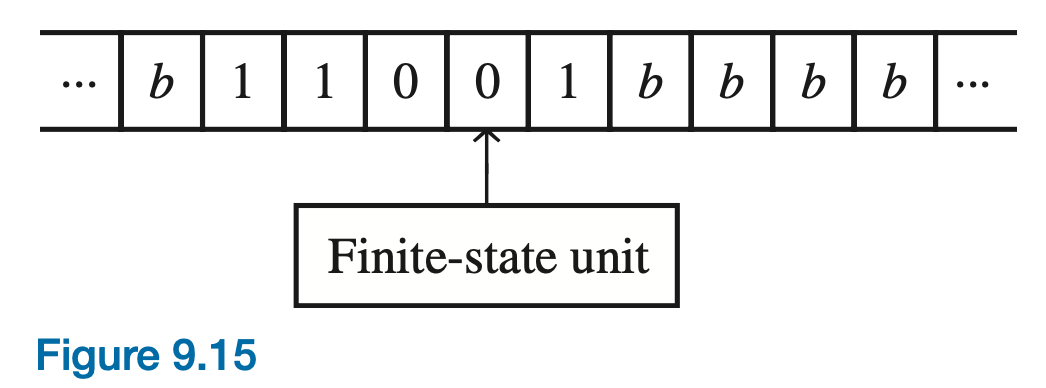
By the next clock pulse, depending on the present state of the unit and the symbol read, the unit either does nothing (halts) or completes three actions:
1. Print a symbol from the alphabet on the cell read (it might be the same symbol that's already there).
2. Go to the next state (it might be the same state as before)
3. Move the read -- write head one cell left or right.
We can describe the actions of any particular Turing machine by a set of quintuples of the form (s,i,i',s',d) , where s and i indicate the present state and the tape symobl being read, i' denotes the symbol printed, s' denotes the new state, and d denotes the direction in which the read-write head moves (R for ight, L for left).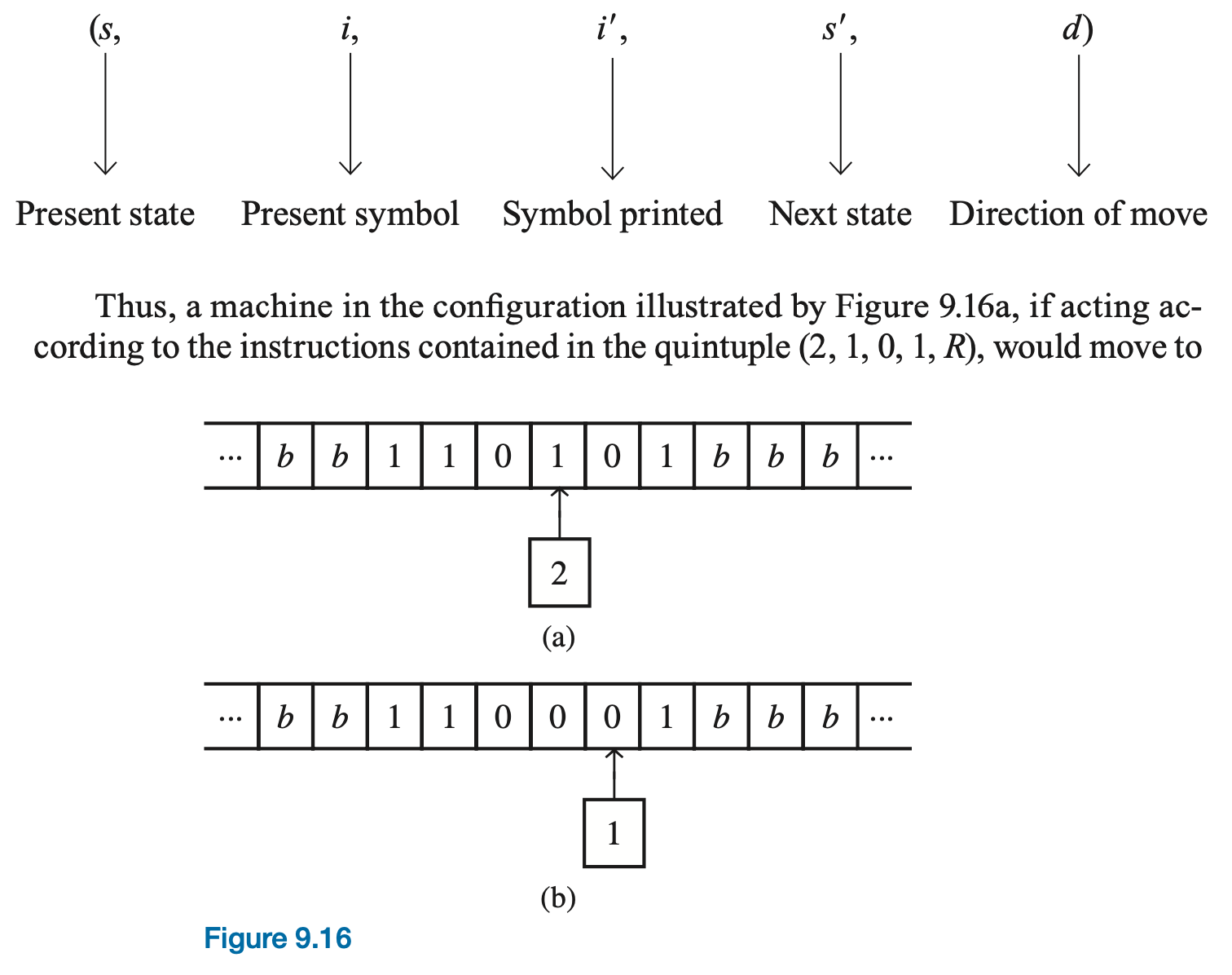
the configuration illustrated in Figure 9.16b. The symbol 1 being read on the tape has been changed to a 0, the state of the unit has been changed from 2 to 1, and the head has moved one cell to the right.
Definition
The restriction that no two quintuples begin with the same s and i symbols ensures that the action of the Turing machine is deterministic and completely specified by its present state and symbol read. If a Turing machine gets into a configuration for which its present state and symbol read are not the first two symbols of any quintuple, the machine halts.
Just as in the case of ordinary finite-state machines, we specify a fixed starting state, denoted by 0, in which the machine begins any computation. We also assume an initial configuration for the read-write head, namely, a position over the farthest left nonblank symbol on the tape. (If the tape is initially all blank, the read-write head can be positioned anywhere to start.)
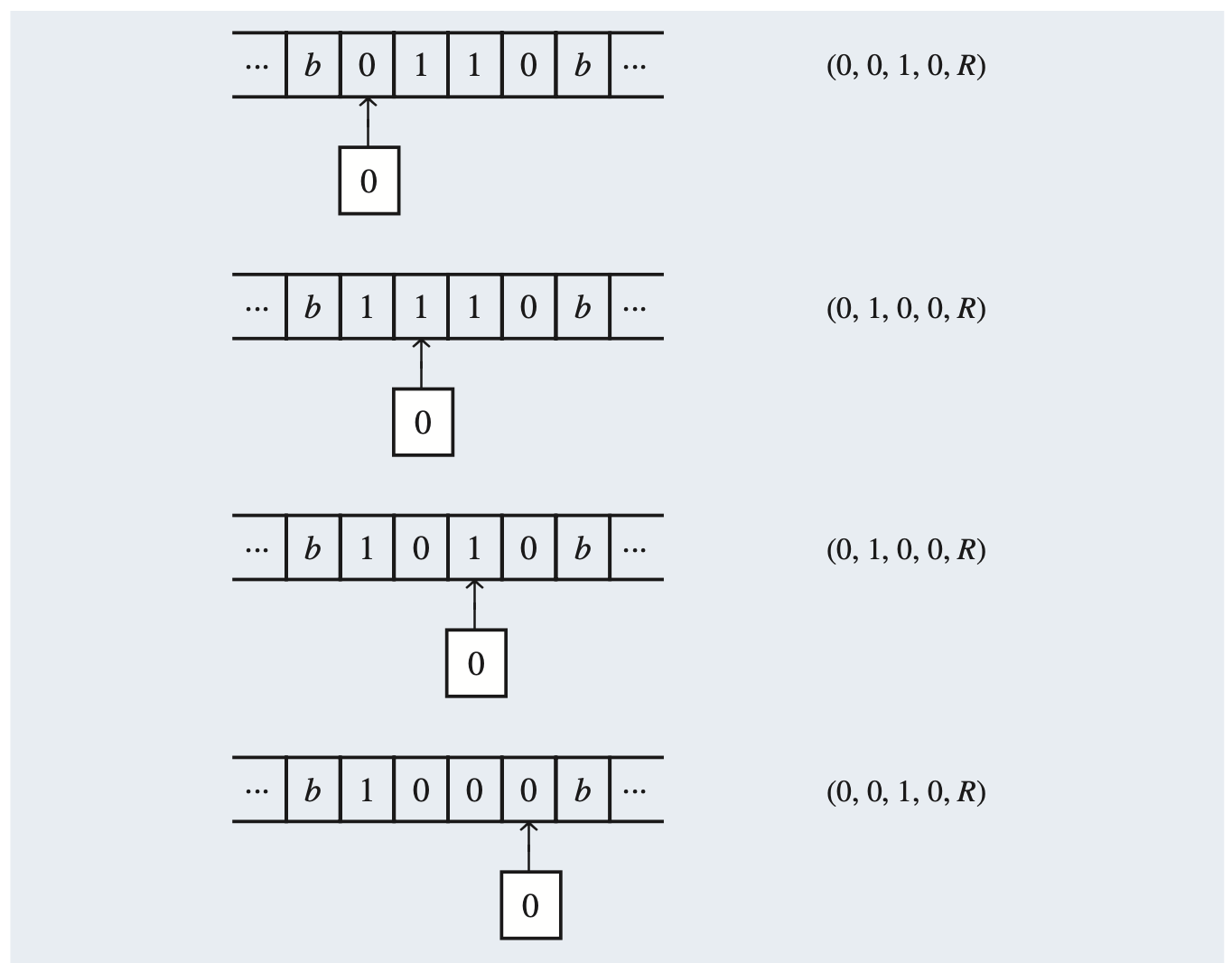
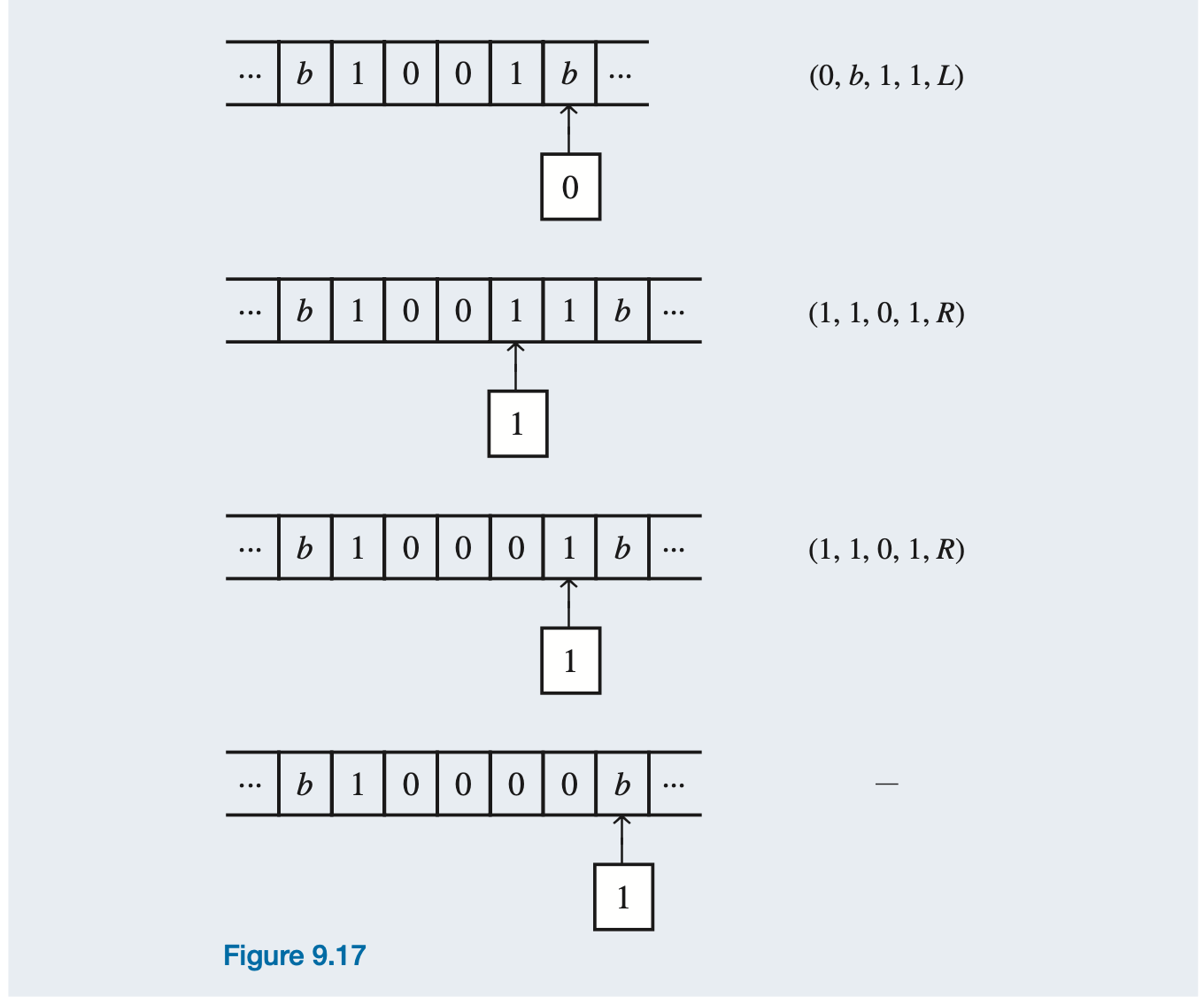
The tape serves as a memory medium for a Turing machine, and in general, the machine can reread cells of the tape. Since it can also write on the tape, the nonblank portion of the tape can be as long as desired, although there are still only a finite number of nonblank cells at any time. Hence the machine has available an unbounded, though finite, amount of storage. Because Turing machines overcome the limitations of finite-state machines, Turing machines should have considerably higher capabilities. In fact, a finite-state machine is a very special case of a Turing machine, one that always prints the old symbol on the cell read, always moves to the right, and always halts on the symbol b.
Practice 57
Why do we study Turing Machines?
1. Defines Computability
- The Turing machine concept answers fundamental questions like "What problems can be solved by a computer?" and "What problems cannot be solved?"
- Some problems are undecidable, meaning no algorithm (or program) can ever solve them. Turing machines help us identify these boundaries, which is crucial in fields like artificial intelligence, cryptography, and optimization.
2. Foundation of Algorithms and Complexity
- Concepts like Big O notation (for algorithm efficiency) and P vs NP problems (for understanding complex problems) are built on ideas from Turing machines.
- Turing machines give us a basic model of computation that all computers can follow. Any algorithm you write, no matter how complex, can theoretically be executed on a Turing machine.
Turing machines can solve a wide range of problems, here are the main types of problems that can be solved by a Turing machine:
1. Decidable Problems
- Arithmetic calculations: Any standard arithmetic operation (addition, subtraction, multiplication, etc.) can be solved.
- Sorting and searching: Sorting a list of numbers, finding an item in a sorted list, and similar tasks are solvable by an algorithm.
- Graph traversal: Problems like finding the shortest path in a graph (Dijkstra’s algorithm) or determining if two nodes are connected.
2. Optimization Problems (within bounds)
- Shortest path problems: Finding the shortest route in a network.
- Scheduling problems: Optimizing tasks over time given certain constraints (e.g., job scheduling in processors).
Problems that Are Not Solvable by a Turing Machine:
1. Unsolvable or Undecidable Problems
- The Halting Problem: Determining whether any given program will halt or run forever.
We study Turing Machines because they provide a theoretical framework for understanding the nature of computation and the limits of what can be computed. They were first described by Alan Turing in 1936, and they have become a fundamental concept in the field of theoretical computer science. They are used to model the behavior of algorithms and to analyze the computability of different problems. Additionally, they serve as a foundation for the theory of complexity, which is used to study the efficiency of algorithms and the resources required to solve different problems. Overall, studying Turing Machines helps us understand the capabilities and limitations of computers and computation.
It's important to note that although Turing Machines may not be directly implemented in physical form, their concepts and principles have influenced the design and development of real-world computers and programming languages. Turing's work laid the groundwork for the development of modern computing and provided invaluable insights into the theoretical underpinnings of computation.
Reference
Life of AlanTuringA.M. Turing Award
Computing Machinery and Intelligence
Brilliant
Stanford Encyclopedia of Philosophy