Chapter 6: Graphs and Trees
Section 6.2 Trees and Their Representations
Tree Traversal Algorithms
If a tree structure is being used to store data, it is often helpful to have a systematic mechanism for writing out the data values stored at all the nodes, which can be accomplished by traversing the tree, that is, visiting each of the nodes in the tree structure. Tree traversal refers to the process of visiting all the nodes of a tree in a specific order. The three common tree traversal algorithms are preorder , inorder , and postorder traversal.The terms preorder, inorder, and postorder refer to the order in which the root of a tree is visited compared to the subtree nodes.
Preorder Traversal
In preorder traversal , the root of the tree is visited first and then the subtrees are processed left to right, each subtree is also traversed in preorder.
Inorder Traversal
In inorder traversal , the left subtree is processed by an inorder traversal, then the root is visited, and then the remaining subtrees are processed from left to right, each in inorder. If the tree is a binary tree, the result is that the root is visited between the processing of the two subtrees. In a nonbinary tree, if there is a single subtree joined to its parent by a vertical arc, that is considered the left subtree and there are no additional subtrees.
Postorder Traversal
In postorder traversal , the root is visited last, after all subtrees have been processed from left to right in postorder.
Reminder
For Binary Tree:Preorder: root, left, right
- ♣ 1. Visit the root.
- ♣ 2. Traverse the left subtree.
- ♣ 3. Traverse the right subtree.
Inorder: left, root, right
- ♣ 1. Traverse the left subtree.
- ♣ 2. Visit the root.
- ♣ 3. Traverse the right subtree.
Postorder: left, right, root
- ♣ 1. Traverse the left subtree.
- ♣ 2. Traverse the right subtree.
- ♣ 3. Visit the root.
For Tree with three Children:
Preorder: root, left, middle, right
Inorder: left, root, middle, right
Postorder: left,middle, right, root
Example
(1) For the binary tree of Figure 6.45: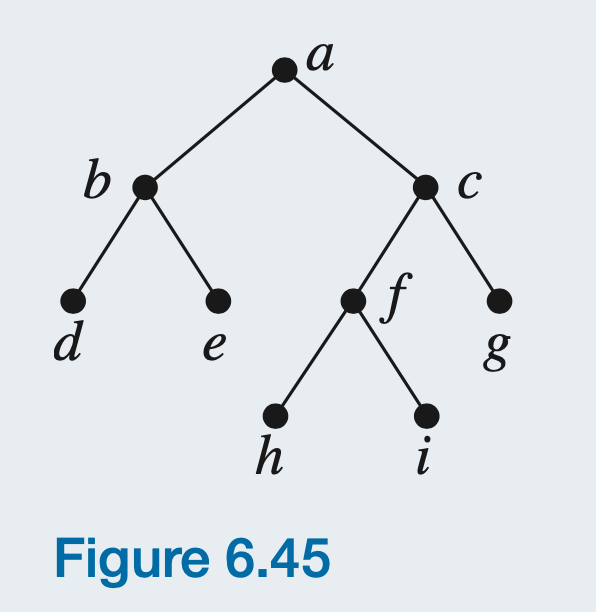
Preorder Traverse:
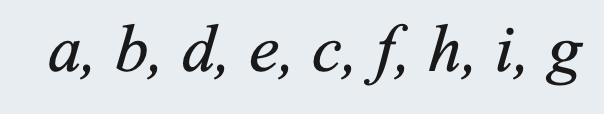
Inorder Traverse:
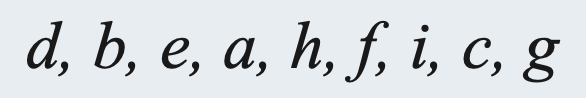
Postorder Traverse:
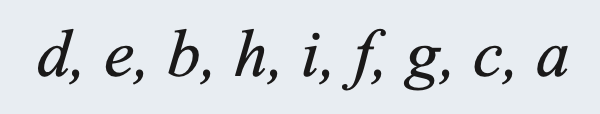
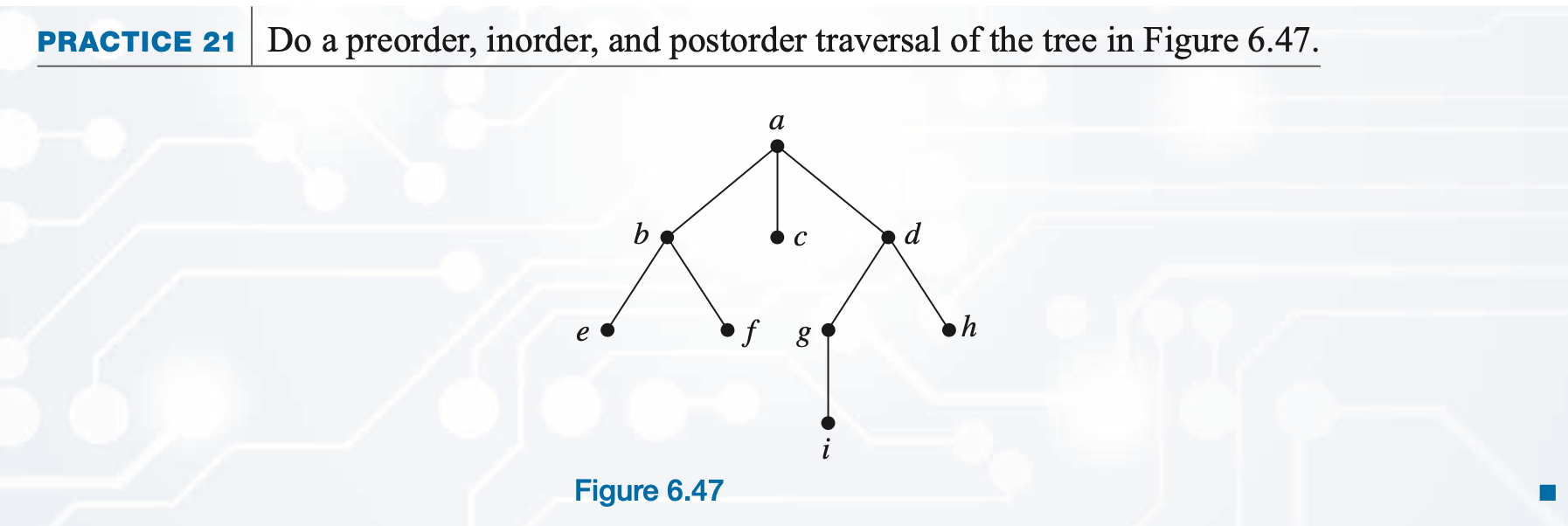
(2) For the tree in Figure 6.46, which is not a binary tree.
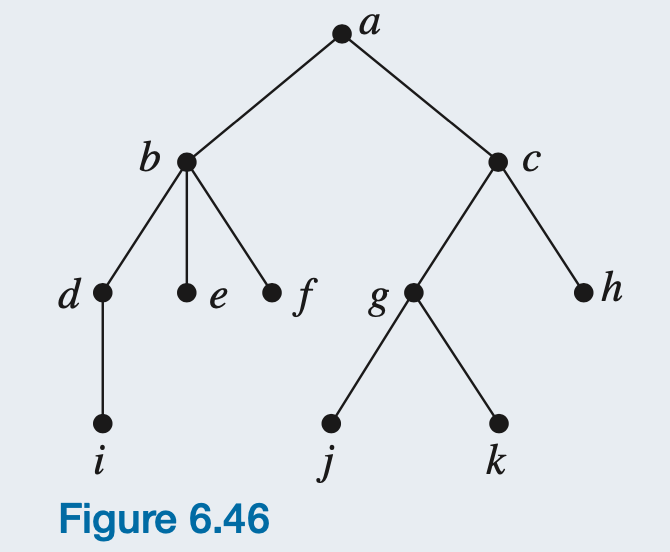
Preorder Traverse:
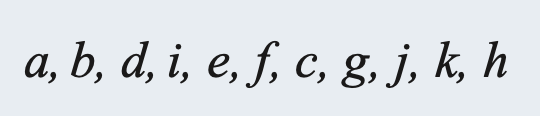
Inorder Traverse:
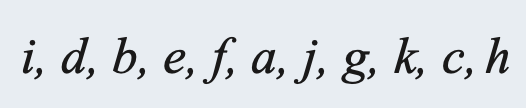
Postorder Traverse:
InOrder.cpp
Summary Table: Choosing the Right Traversal
| Tree Type | Preorder | Inorder | Postorder | DFS | BFS (Level-Order) |
|---|---|---|---|---|---|
| Binary Tree (2 children) | ✅ Yes | ✅ Yes | ✅ Yes | ✅ Yes | ✅ Yes |
| Ternary Tree (3 children) | ✅ Yes | ✅ Yes (Left → Root → Middle → Right) | ✅ Yes | ✅ Yes | ✅ Yes |
| General N-ary Tree (>3 children) | ✅ Yes | ❌ Not Well-Defined | ✅ Yes | ✅ Yes | ✅ Yes |
Practice
Algebraic Experssion Tree

Practice
Please draw the algebraic expression tree for the following expression: $$ (4x^2-3z)*(5x+7) $$ Please traverse the tree using preorder, inorder and postorder algorithms.Summary Table: When to Use Prefix, Infix, and Postfix
| Notation | Order (Traversal) | Used For |
|---|---|---|
| Prefix (+ 3 5) | Root --> Left --> Right (Preorder Traversal) | Expression Parsing, LISP Programming, Polish Notation |
| Infix (3 + 5) | Left --> Root --> Right (Inorder Traversal) | Human-Readable Expressions, Algebra, Programming Languages |
| Postfix (3 5 +) | Left --> Right --> Root (Postorder Traversal) | Expression Evaluation, Compilers, Stack-Based Calculators |
For modern scientific calculators:
- ♣ 1. Humans enter expressions using Infix notation (e.g., 3 + 5 * 2).
- ♣ 2. Internally, the calculator converts the infix expression to Postfix to evaluate it efficiently.
- ♣ 3. The final result is computed using stack-based evaluation and displayed to the user.