Chapter 9: Finite-State Machines, Turing Machines
Section 9.4 Turing Machines
We have spent quite a bit of time discussing what Turing machines can do. By the Church–Turing thesis, they can do a great deal indeed, although not very efficiently. It is even more important, however, to consider what Turing machines cannot do. Because a Turing machine’s abilities to perform tasks exceed those of an actual computer, if we find something no Turing machine can do, then a real computer cannot do it either. In fact, by invoking the Church–Turing thesis, no algorithm exists to do it, and the task is not computable. The type of task we have in mind here is generally that of determining the truth value of each of a number of related statements.
Halting Problem
The halting problem asks whether it is possible to write a program that can determine, for any given program and input, whether that program will halt (terminate) or continue running indefinitely. In other words, it is a decision problem that seeks to determine if a program will reach a stopping point or run forever. The significance of the halting problem lies in its negative answer. Alan Turing showed that there is no algorithmic solution to the halting problem: it is undecidable. This means that there is no general-purpose algorithm or computer program that can correctly determine whether an arbitrary program will halt or not for all possible inputs. This has profound implications for computer science because it shows that there are inherent limits to what can be computed algorithmically. It demonstrates that there are problems that simply cannot be solved by any computer program, regardless of its computational power. The undecidability of the halting problem highlights the existence of fundamental limitations in our ability to reason about program behavior and predict their outcomes. The halting problem has also led to further developments in computability theory, such as the notion of Turing completeness and the classification of problems into different complexity classes (like the famous P and NP classes). It serves as a cornerstone for understanding the boundaries of what is computationally possible and has influenced various areas of computer science, including programming languages, compiler design, and formal verification techniques.
In simpler terms, the Halting Problem is about whether a computer program can analyze another program and accurately predict whether it will stop running or continue running forever. This problem is important because it touches on the limits of what computers can and cannot do.

Question:
Can we create a program that checks whether any program will stop or run forever?Answer:
No, Alan Turing proved it’s impossible. It’s undecidable.👉 This teaches us: Not everything is solvable. There are limits to what computers can do.
If problems are solvable, how hard are they?
This moves us into complexity theory, which studies how much time, space, and work it takes to solve problems.
Computational Complexity
The Halting Problem has catalyzed advancements in computational complexity theory. This branch of theoretical computer science studies the resources required to solve computational problems, such as time and space.The Halting Problem has had a significant influence on the classification of computational problems based on their complexity, leading to the establishment of important complexity classes such as:
- P
- NP
- NP-complete
- NP-hard
As a model of computation, the Turing machine has provided us with a way to prove the existence of unsolvable (uncomputable) problems. Not only does the Turing machine help us find the limits of computability, but it can also help us classify problems that are computable—that have an algorithm for their solution by the amount of work required to carry out the algorithm.
P, NP, NP-Complete and NP-Hard Problems in Computer Science
In theoretical computer science, the classification and complexity of common problem definitions have two major sets; P which is "Polynomial" time and NP which is "Non-deterministic Polynomial" time. There are also NP-Hard and NP-Complete sets, which we use to express more sophisticated problems. In the case of rating from easy to hard, we might label these as "easy", "medium", "hard", and finally "hardest":P

P is a set of problems that can be solved (deterministic) in Polynomial Time.
NP

NP is a set of problems that can be solved in non-polynomial time (typically requiring much more time than polynomial algorithms, such as exponential time), but whose solutions can be verified in polynomial time. (eg: Sudoku)
NP-Complete
NP-Complete problems are the hardest problems inside NP.This means they satisfy two important conditions:
- ☆ In NP: Their solutions can be verified in polynomial time (easy to check once someone gives you a solution).
- ☆ In NP-Hard: They are at least as hard as every problem in NP — meaning if you can solve one NP-Complete problem quickly (in polynomial time), you can solve all NP problems quickly. (No such algorithm has been found yet)
NP-Hard
NP-Hard is a set of problems that are at least as hard as the hardest problems in NP. Unlike NP-Complete problems, NP-Hard problems do not need to be in NP—meaning they might not even have a polynomial-time verification method. Some are even undecidable, meaning no algorithm can solve them even with unlimited time and resources.The Standard Relationship Between P, NP, NP-Complete, NP-Hard
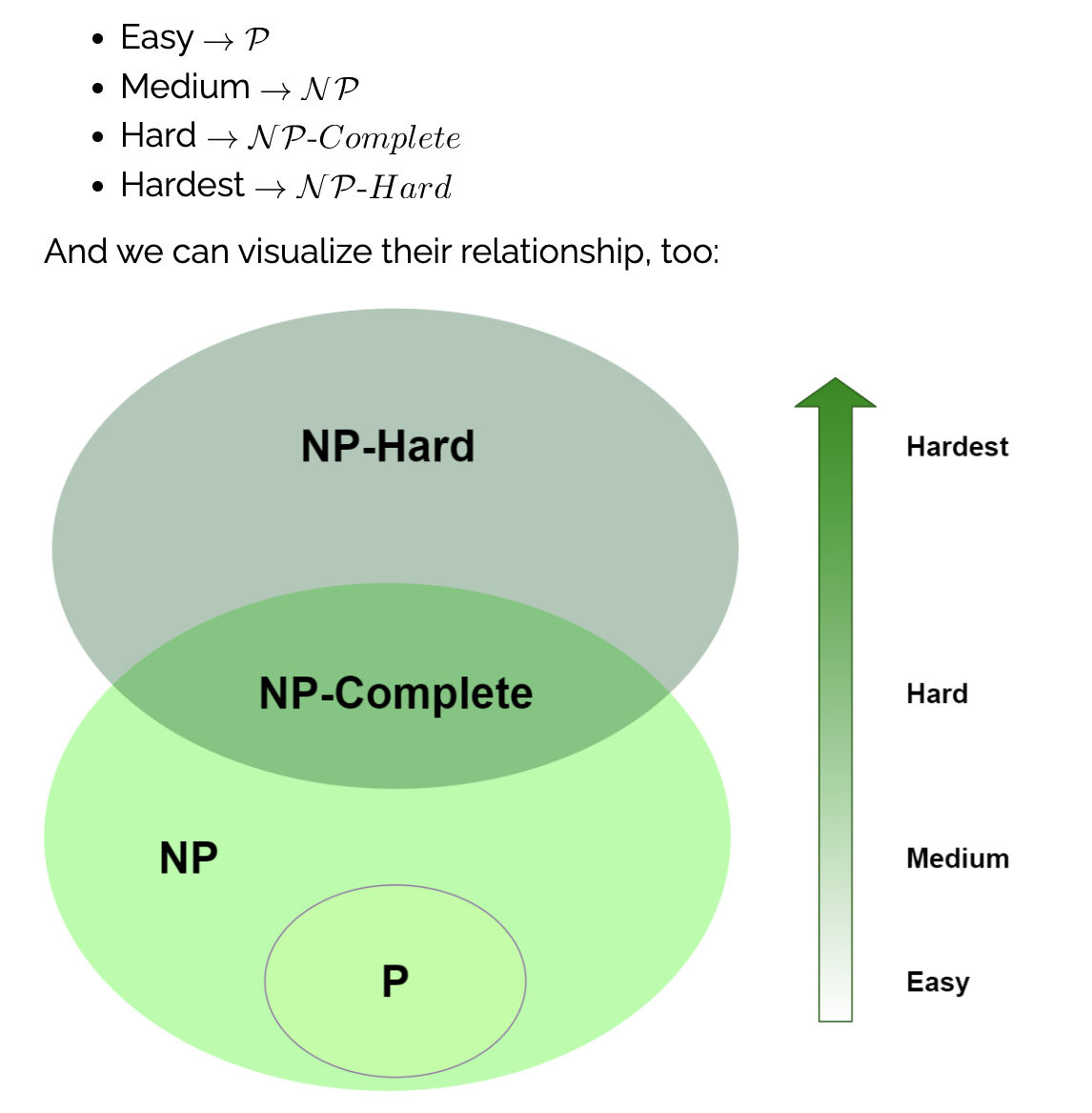
Comparison of P, NP, NP-Complete, and NP-Hard
| Class | Solve Quickly (Polynomial Time)? | Verify Quickly (Polynomial Time)? | Must Be in NP? | Hardness | Examples |
|---|---|---|---|---|---|
| P | ✅ Yes | ✅ Yes | ✅ Yes | Easy | Sorting numbers, Dijkstra’s algorithm |
| NP | ❓ Maybe hard to solve | ✅ Yes | ✅ Yes | Harder than P | Sudoku, Hamiltonian Path |
| NP-Complete | ❌ Hard to solve | ✅ Yes | ✅ Yes | Hardest in NP | Traveling Salesman (decision version), Knapsack (decision version) |
| NP-Hard | ❌ Hard to solve | ❓ Maybe not even verifiable | ❌ No | At least as hard as NP problems (or harder) | Halting Problem, TSP (optimization version) |
Big-O Notation
Big-O notation is used to analyze the time complexity (how the running time of an algorithm increases with input size) and space complexity (how the memory usage of an algorithm increases with input size) of algorithms.- O(1) - constant time (The running time or space usage of the algorithm remains constant regardless of the input size.) (Example: accessing a specific element in an array.)
- O(\(log_2(n)\)) - logarithmic time (The running time or space usage grows logarithmically with the input size.) (Example: binary search )
- O(n) - linear time (The running time or space usage grows linearly with the input size.) (Example: linear search)
- O(\(n^2\)) - quadratic time (The running time or space usage grows quadratically with the input size.) (Example: nested loops )
- O(\(n^k\)) - polynomial time with an exponent k greater than 2 (The runtime or space grows polynomially with the input size,
where k is the degree of the polynomial.) (Example: Matrix Multiplication) - O(\(k^n\)) - exponential time (The running time or space usage grows exponentially with the input size.) (Example: Hamiltonian Circuit)
- O(n!) - factorial-time (The running time or space usage grows factorially with the input size.) (Example: Traveling Salesman Problem (TSP) - Brute Force Solution)
Polynomial Algorithms
The first set of problems are polynomial algorithms that we can solve in polynomial time, like logarithmic, linear or quadratic time.eg: Linear Search O(n), Bubble Sort (O(n^2)), Merge Sort (O(nlogn)), Djikstra Algorithm, Matrix Multiplication ...
NP Algorithms
The second set of problems cannot be solved in polynomial time. However, they can be verified or certified in polynomial time. We expect these algorithms to have an exponential complexity.eg: Hamiltonian Path, Sudoku Solving, Integer Factorization, Graph Isomorphism,
NP-Complete Algorithms
The next set is very similar to the previous set. Taking a look at the diagram, all of these all belong to NP, but are among the hardest in the set. NP-Complete problems are both in NP and NP-Hard. What makes them different from other NP problems is a useful distinction called completeness. For an NP problem that's complete, there exists a polynomial-time algorithm that can transform the problem into any other NP-complete problem. This transformation requirement is also called reduction. In simpler terms, if we have an efficient algorithm to solve an NP-Complete problem, we can use it to solve any other problem in NP. This means that if any NP-Complete problem can be solved in polynomial time, then all problems in NP can be solved in polynomial time.Despite decades of research, no one has found a polynomial-time algorithm to solve an NP-Complete problem.
eg: Traveling Salesman (decision version), Knapsack (decision version), Graph Coloring ...
NP-Complete is a subset of NP, and it consists of the most difficult problems within NP.
NP-Hard Algorithms
The last set of problems contains the hardest, most complex problems in computer science. They are not only hard to solve but are hard to verify as well. In fact, some of these problems aren't even decidable.eg: K-means Clustering, Traveling Salesman Problem (optimization version), Halting Problem
Conclusion
P problems are quick to solve. NP problems are quick to verify but slow to solve. NP-Complete problems are also quick to verify, slow to solve and can be reduced to any other NP-Complete problem. NP-Hard problems are slow to verify, slow to solve.
P =? NP
Clearly, P ⊆ NP. P is a subset of NP: All problems in P are also in NP. If a problem can be solved in polynomial time, it can certainly be verified in polynomial time.Arguably, the biggest open question in theoretical computer science concerns the relationship between those two classes:
Is P equal to NP?The P vs. NP problem is one of the seven Millennium Prize Problems, with a $1 million reward for its solution. Despite decades of research, it remains unresolved.
Since 2002, William Gasarch has conducted three polls of researchers concerning this and related questions.Confidence that P ≠ NP has been increasing – in 2019, 88% believed P ≠ NP, as opposed to 83% in 2012 and 61% in 2002. When restricted to experts, the 2019 answers became 99% believed P ≠ NP. These polls do not imply anything about whether P = NP is true, as stated by Gasarch himself: "This does not bring us any closer to solving P=?NP or to knowing when it will be solved, but it attempts to be an objective report on the subjective opinion of this era."
Millennium Prize Problems
Millennium Prize ProblemsReference
Hard Problems in Computer ScienceP versus NP problem