Chapter 6: Graphs and Trees
Section 6.1 Graphs and Their Representations
Graph Terminology
Graphs are formal mathematical representations of networks, collections of objects, events, or set elements that lead naturally from one to another.Before proceeding, we need some terminology about graphs. Surprisingly, although there is a large body of literature in graph theory, the terminology is not completely standard. Therefore other books may give slightly different variations of some of these terms.
Adjacent Vertices
Two vertices are said to be adjacent if there is an edge(arc) connecting them.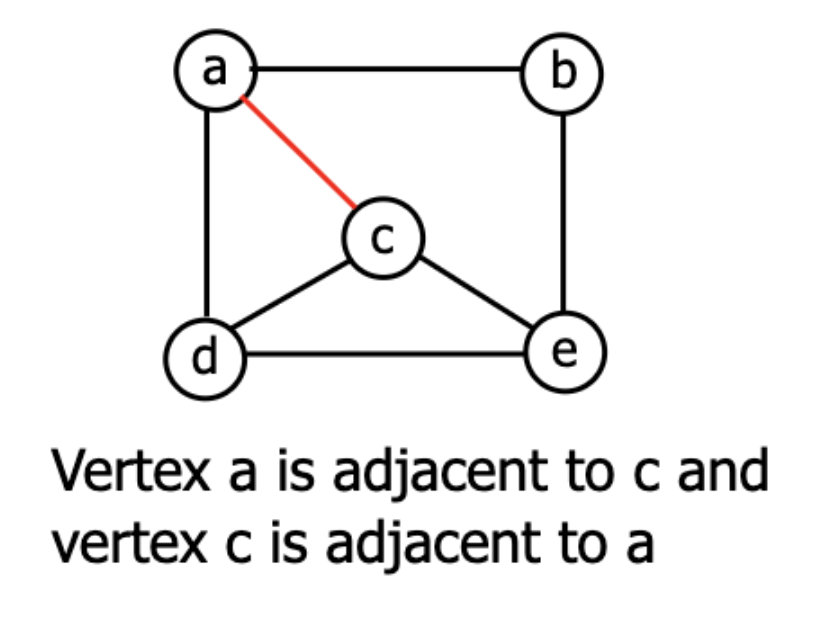
Adjacent Edges
Adjacent edges are edges that share a common vertex.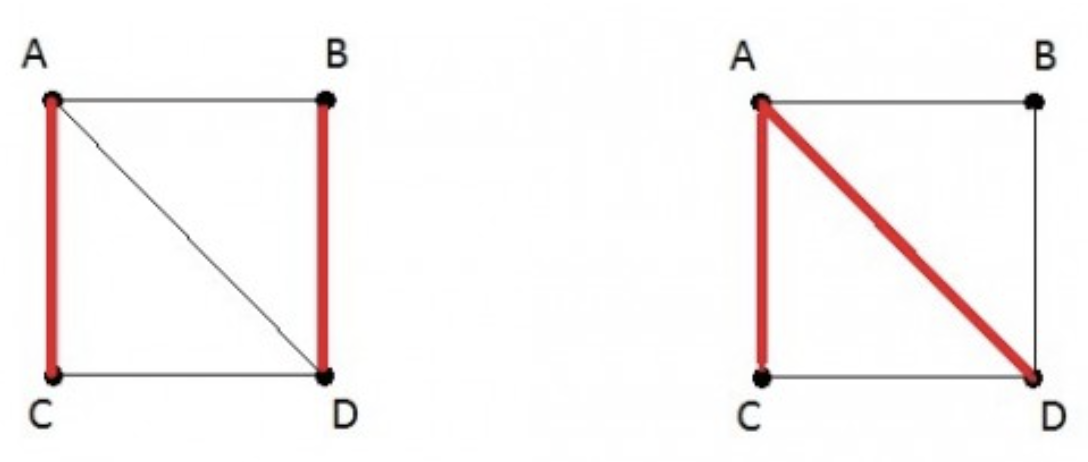
(2) Edge (A,C) and (B,D) are not adjacent edges, they don't have common vertex.
Loop
A loop is an edge that connects a vertex to itself. A graph with no loops is loop free .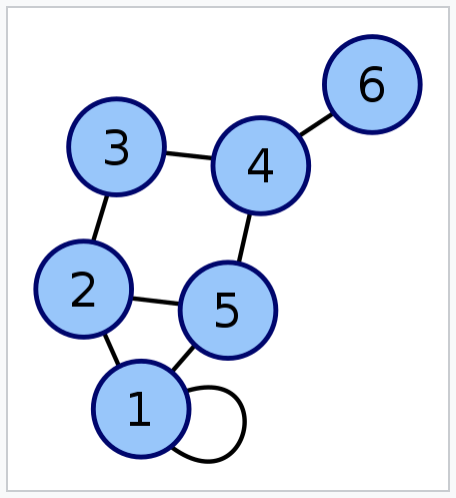
Application in Real-World of Loop:
- Self-Loops in Social Networks: On social media platforms like Twitter, a user might retweet their own tweet or interact with their own posts (like, comment, or share). This can be thought of as a loop in a social network graph, where a user (vertex) interacts with themselves (edge connecting back to the same vertex).
- Personal Communication: In a social graph, a loop could represent an individual calling or texting their own number (e.g., testing a phone system) or sending an email to themselves.
Parallel Arcs
Two arcs with the same endpoints are parallel arcs . Parallel arcs share the same pair of start and end vertices.
Application in Real-World of Parallel Arcs:
- Flight Routes: In airline networks, parallel arcs can represent multiple airlines operating flights between the same two airports. For example, if both Delta and American Airlines offer flights between JFK and LAX, the two flight routes form parallel arcs in the network.
- Electrical Circuits: In circuit design, parallel wires connecting the same two components (like resistors, capacitors, or power sources) create parallel arcs, offering multiple paths for current to flow.
Simple Graph
A simple graph is an unweighted, undirected graph that does not have more than one edge between any two vertices and no edge starts and ends at the same vertex. In other words, a simple graph is a graph without loops and without parallel arcs.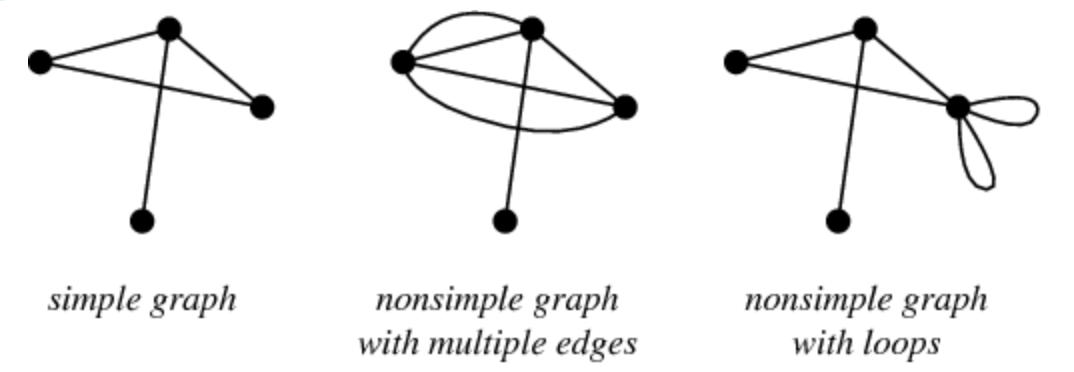
- Unweighted
- Undirected
- No Loops
- No Parallel Arcs
Isolated Node
An isolated node is adjacent to no other node.
Real-World Examples:
- Disconnected House: A house that has been disconnected from the power grid due to an outage or maintenance would be an isolated node in the power distribution network.
- Offline Security Camera: A security camera that is part of a smart home system but currently offline or unconnected to the home network would be an isolated node in the security network.
Degree of a Vertex
The degree of a vertex is the number of arcs incident with that vertex.
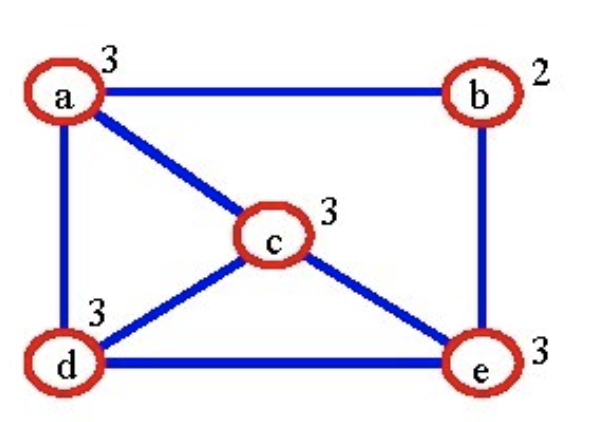
- For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices.
- A special case is a loop, which adds two to the degree. This can be understood by letting each connection of the loop edge count as its own adjacent vertex.
Complete Graph
A complete graph is a simple undirected graph in which each pair of distinct vertices is connected by a unique edge.Complete graphs on \(n\) vertices, for \(n\) between 1 and 12, are shown below along with the numbers of edges:
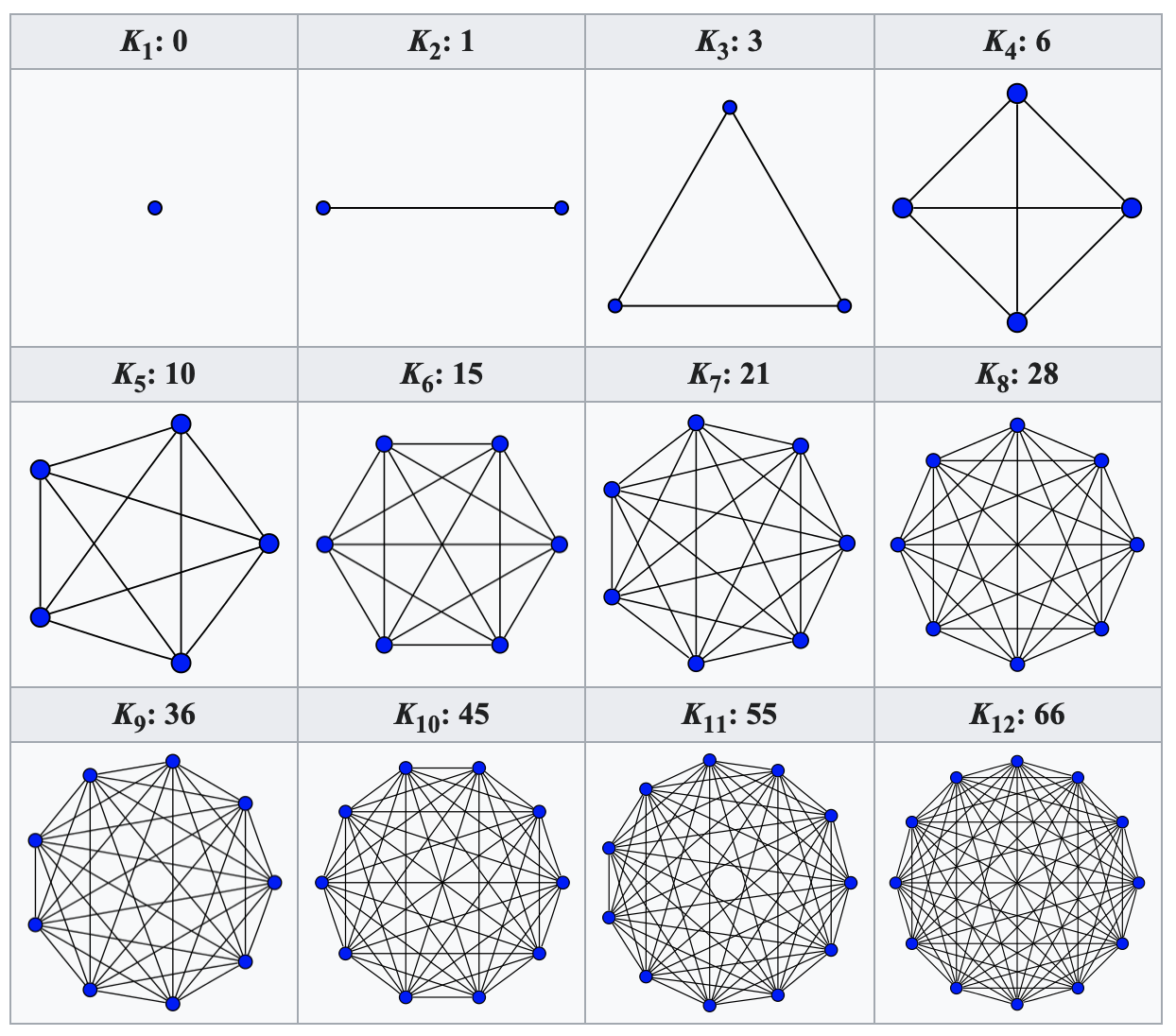
- All Vertices Connected: In a complete graph, every vertex is connected to every other vertex by a single edge. There are no missing connections.
- No Parallel Edges or Loops
- Maximum Number of Edges: A complete graph contains the maximum possible number of edges for a given number of vertices.
\( E(n) = \frac{n(n-1)}{2} \) where:
- \(E(n)\) is the number of edges in the graph.
- \(n\) is the number of vertices in the graph.
Path
A path in a graph represents a way to get from an origin to a destination by traversing edges in the graph. For example, in the undirected graph G = (V,E) drawn below, there are many paths from node 6 to node 1. One such path is highlighted with red:
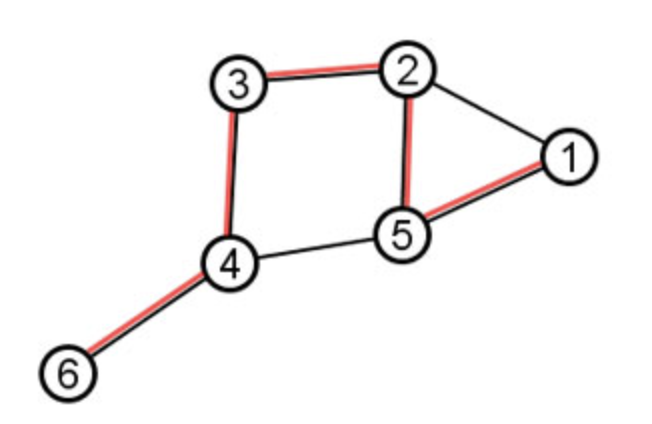
A path is a sequence of vertices with the property that each vertex in the sequence is adjacent to the vertex next to it. A path that does not repeat vertices is called a simple path . A path from node \(n_0\) to node \(n_k\) is a sequence \(n_0, a_0, n_1, a_1, \dots, n_{k-1}, a_{k-1}, n_{k}\) of nodes and arcs where for each \(i\), the endpoints of arc \(a_i\) are \(n_i - n_{i+1}\)
Length of a Path
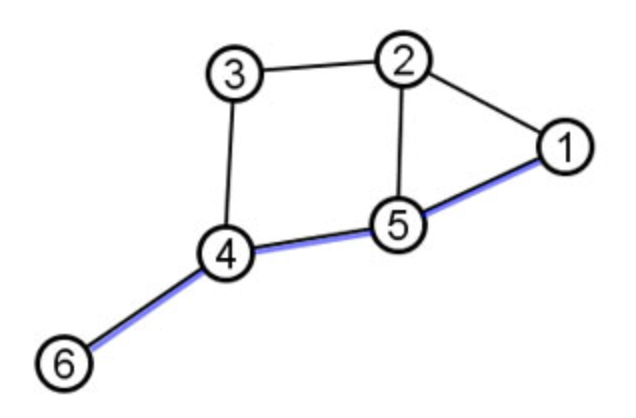
The length of a path is the number of arcs it contains; if an arc is used more than once, it is counted each time it is used.Connected Graph
A graph is connected if there is a path from any node to any other node.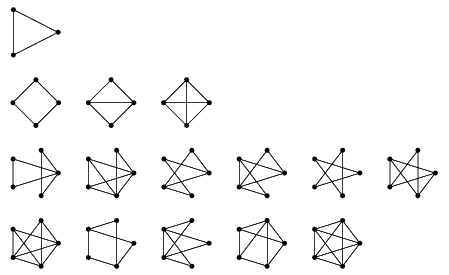
Applications of Connected Graphs:
- Networking: In computer and communication networks, a connected graph ensures that every device (node) can communicate with every other device.
- Transportation Systems: Road networks are modeled as connected graphs to ensure that all locations can be reached from any starting point.
Cycle
A cycle in a graph is a path from some node \(v_0\) back to \(v_0\) where no arc appears more than once in the path sequence, \(v_0\) is the only node appearing more than once, and \(v_0\) occurs only at the ends. A graph with no cycles is acyclic .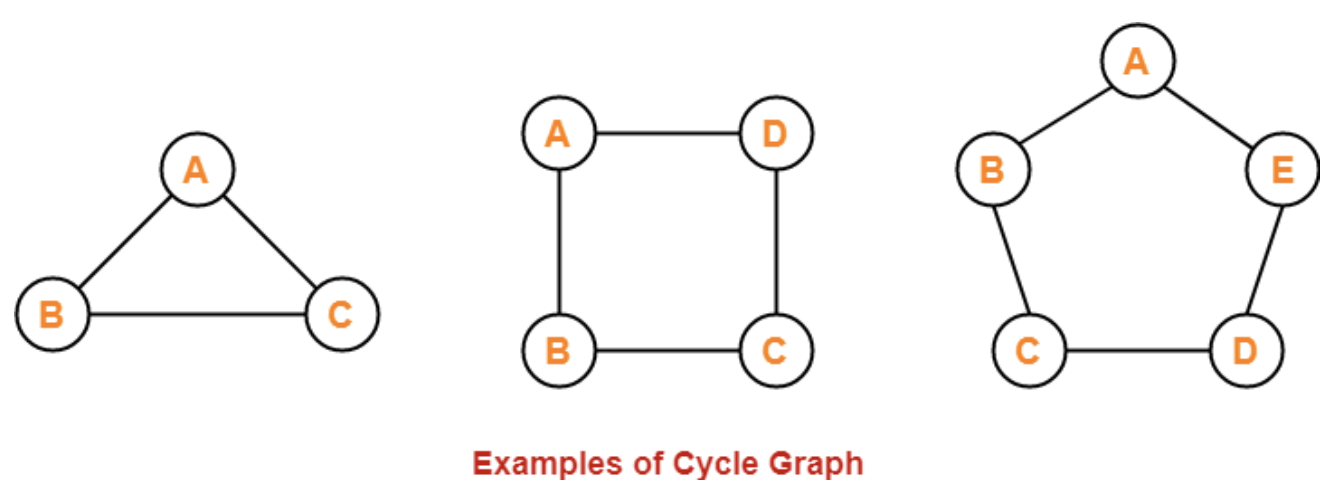
- \(v_0, v_1, ..., v_n\) are vertices in the graph.
- Each consecutive pair of vertices \((v_i,v_{i+1})\) is connected by an edge in the graph.
- The path forms a loop, meaning it starts and ends at the same vertex:\(v_0 = v_n\)
- No other vertex repeats within the sequence except for the start and end vertex.
Bipartite Complete Graph
A graph is a bipartite complete graph if its nodes can be partitioned into two disjoint nonempty sets \(N_1\) and \(N_2\) such that two nodes \(x\) and \(y\) are adjacent if and only if \(x ∈ N_1\) and \(y ∈ N_2\). If \(|N_1| = m\) and \(|N_2| = n\), such a graph is denoted by \(K_{m,n}\). It is a special kind of bipartite graph where every vertex to the first set is connected to every vertex of the second set.In such a graph, every vertex from one set is connected to every vertex from the other set, but there are no edges between vertices within the same set.
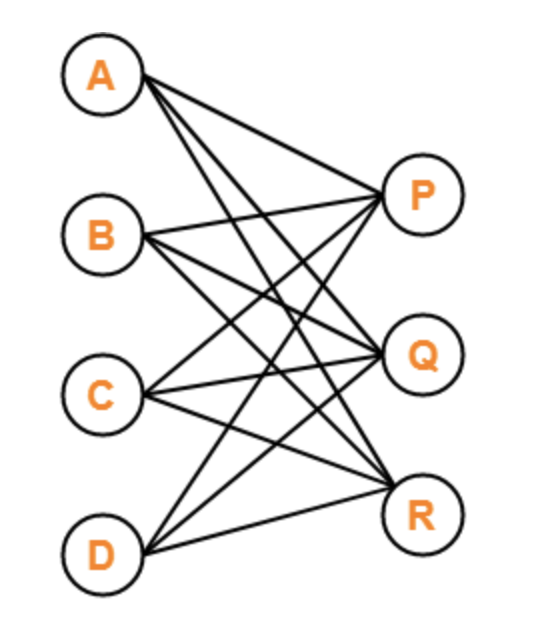
- Two Disjoint Sets:The graph is bipartite, meaning its vertex set can be divided into two disjoint sets
- Complete:In a bipartite complete graph, every vertex in set \(N_1\) is connected to every vertex in \(N_2\).
Real-world application for Bipartite Complete Graph
- Airport Networks: In an international airline system, one set can represent airports in country A, and another set can represent airports in country B. In a bipartite complete graph model, every airport in country A has a direct flight to every airport in country B, maximizing connectivity between the two regions.
- Processor-Core Communication: In parallel computing, if every processor in a set needs to communicate with every core in another set, this interaction can be modeled as a bipartite complete graph. This ensures complete communication between the processors and cores, improving task allocation.
Isomorphism Graphs
An isomorphic graphs G and H is a bijection between the vertex sets of G and H.\(f: V(G) → V(H) \)
such that any two vertices \(u\) and \(v\) of G are adjacent in G if and only if \(f(u)\) and \(f(v)\) are adjacent in H. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structrue-perserving bijection.
Two graphs \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) are isomorphic if there is a one-to-one correspondence (or mapping) between their vertex sets and edge sets.
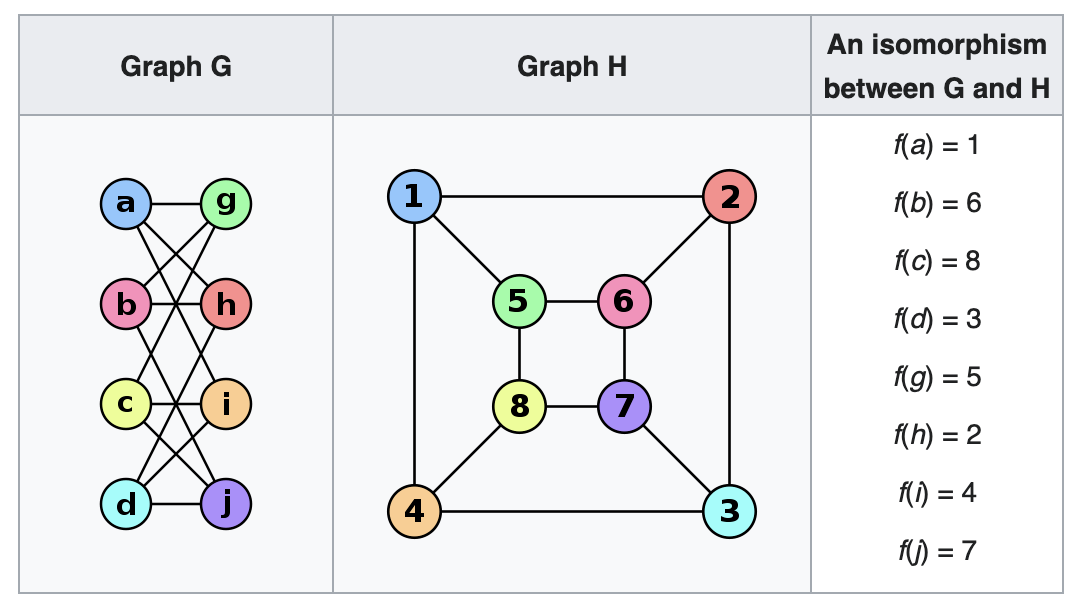
Isomorphism graphs refers to a concept in graph theory where two graphs are considered isomorphic if they are structurally identical, even though their vertex and edge labels might differ.
- Same number of vertices: Both graphs must have the same number of vertices.
- Same number of edges: Both graphs must have the same number of edges.
- Preservation of adjacency: If two vertices are connected by an edge in one graph, their corresponding vertices in the other graph must also be connected.
How can we check if two graphs are isomorphic?
- 1. Compare the Number of Vertices and Edges Count the number of vertices and edges in both graphs.
- 2. Compare the Degree of Each Vertex For each graph, calculate the degree of each vertex.
- 3. Compare Neighborhoods Compare the local neighborhoods of vertices.
- 4. Use algorithms for larger graphs.
If the number of vertices or edges is different, the graphs are not isomorphic.
If the degree sequences (the list of vertex degrees) are not the same in both graphs, they are not isomorphic.
If a vertex in one graph is connected to a set of vertices, the corresponding vertex in the other graph must have the same neighborhood structure.
Graph Isomorphism in Real-World Applications:
- Pattern Recognition: Isomorphism is used in computer vision and pattern recognition to determine if two objects or structures are the same under relabeling or rotation.
- Chemical Structures: In chemistry, graph isomorphism helps in identifying whether two molecular structures (represented as graphs) are identical, regardless of atom labeling.
Practice
(1) Sketch a graph having nodes {1,2,3,4,5}, arcs {{1,2}, {1,3}, {3,4}, {3,4}, {4,5}, {5,5}}(2) Refer to the graph created in Practice 1.
a. Find two nodes that are not adjacent. b. Find a node adjacent to itself. c. Find a loop. d. Find two parallel arcs. e. Find the degree of node 3. f. Find a path of length 5. g. Find a cycle. h. Is this a graph complete? i. Is this graph connected?