Chapter 6: Graphs and Trees

Section 6.1 Graphs and Their Representations



Graphs are a fundamental concept in discrete mathematics that represent relationships between objects. They are widely used in computer science, transportation, social networks, chemistry, and artificial intelligence. This section explains what graphs are, their different types, and their representations.

Graph and Their Representations

Graphs are formal mathematical representations of networks, collections of objects, events, or set elements that lead naturally from one to another.

Graph (Informal Definition)

A graph is a collection of nodes (vertices) connected by edges (arcs). These connections represent relationships between entities. A graph is a nonempty set of nodes(vertices) and a set of arcs(edges) such that each arc connects two nodes.
Our graphs will always have a finite number of nodes and arcs.

Example 1: Graph Representing Cities

This graph visually represents airline connections between major cities. In the graph below, the vertices represents the cities, and the edges are the distance between them.

The set of nodes in the airline map of Figure 1 is {Singapore, Tokyo, Hong Kong, Detroit, Austin, Washington, Seattle, San Francisco}. There are 12 arcs; Singapore-Tokyo is an arc (here we are naming an arc by the nodes it connects), Detroit-Austin is an arc, and so on.

Figure 1

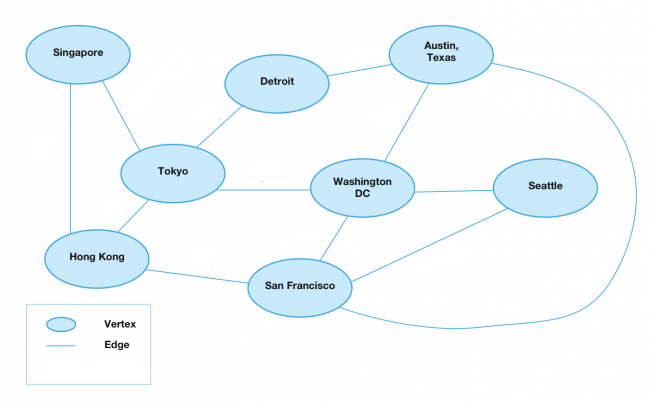
The informal definition of a graph works quite well if we have the visual representation of the graph before us to show which arcs connect which nodes. Without the picture, however, we need a concise way to convey this information. Hence our second definition of a graph.

Graph (Formal Definition)

A graph G is an ordered pair G=(V,E) where

• V is a nonempty set of nodes(vertices)

• E is a set of arcs(edges)

• Each edge is a pair of vertices.

In other words, each element of E is a pair of elements of V.

Example 2: Simple Graph Representation

In the graph below, the vertices represents the circles, and the edges are the lines between them.


Figure 2

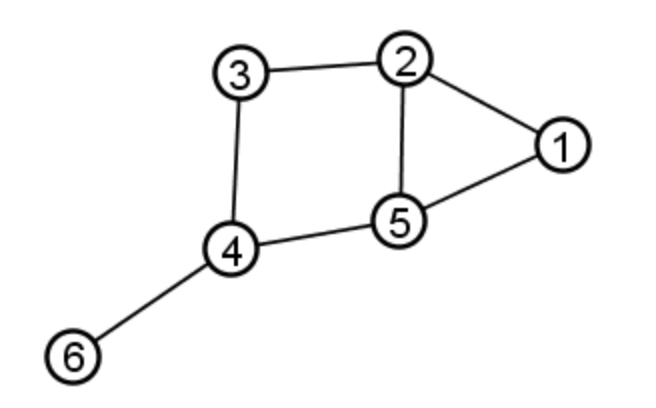
For the graph of Figure 2 represents the following graph:

• V = {1,2,3,4,5,6}

• E = {{1,2}, {1,5}, {2,3}, {2,5} {3,4}, {4,5}, {4,6}}

• G = (V,E)
This graph can represent a network, a road system, or even a social connection.

Undirected and Directed

Undirected graph: An undirected graph has edges with no direction. The edges of a graph are assumed to be unordered pairs of nodes. Sometimes we use an undirected graph to emphasize this point. In an undirected graph, we write edges using curly braces to denote unordered pairs. For example, an undirected edge {2,3} from vertex 2 to vertex 3 is the same thing as an undirected edge {3,2} from vertex 3 to vertex 2.

Direct graph: A directed graph (digraph) has edges with a direction. In a directed graph, the two directions are counted as being distinct directed edges. In a directed graph, we write edges using parentheses to denote ordered pairs. For example, edge (2,3) is directed from 2 to 3, which is different than the directed edge (3,2) from 3 to 2. Directed graphs are drawn with arrowheads on the links, as shown below:


Figure 3

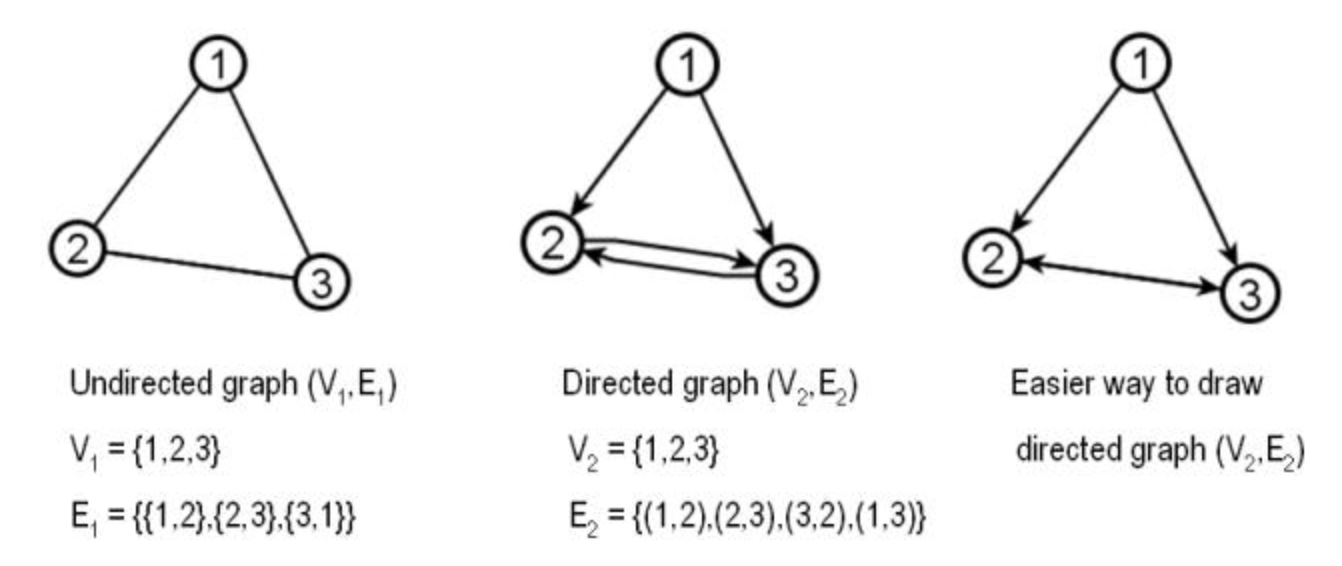
In this class, the term "graph" will mean an undirected graph. To refer to a directed graph, we will always say "directed graph".

Labeled Graph and Weighted Graph

Besides imposing direction on the arcs of a graph, we may want to modify the basic definiton of a graph in other ways. We often want the nodes of a graph to carry identifying information, like the names of the cities in the map of airline routes. This map would be a labeled graph . We may want to use a weighted graph , where each arc has some numerical value, or weight, associated with it. For example, we might want to indicate the price of the various routes in the airline map.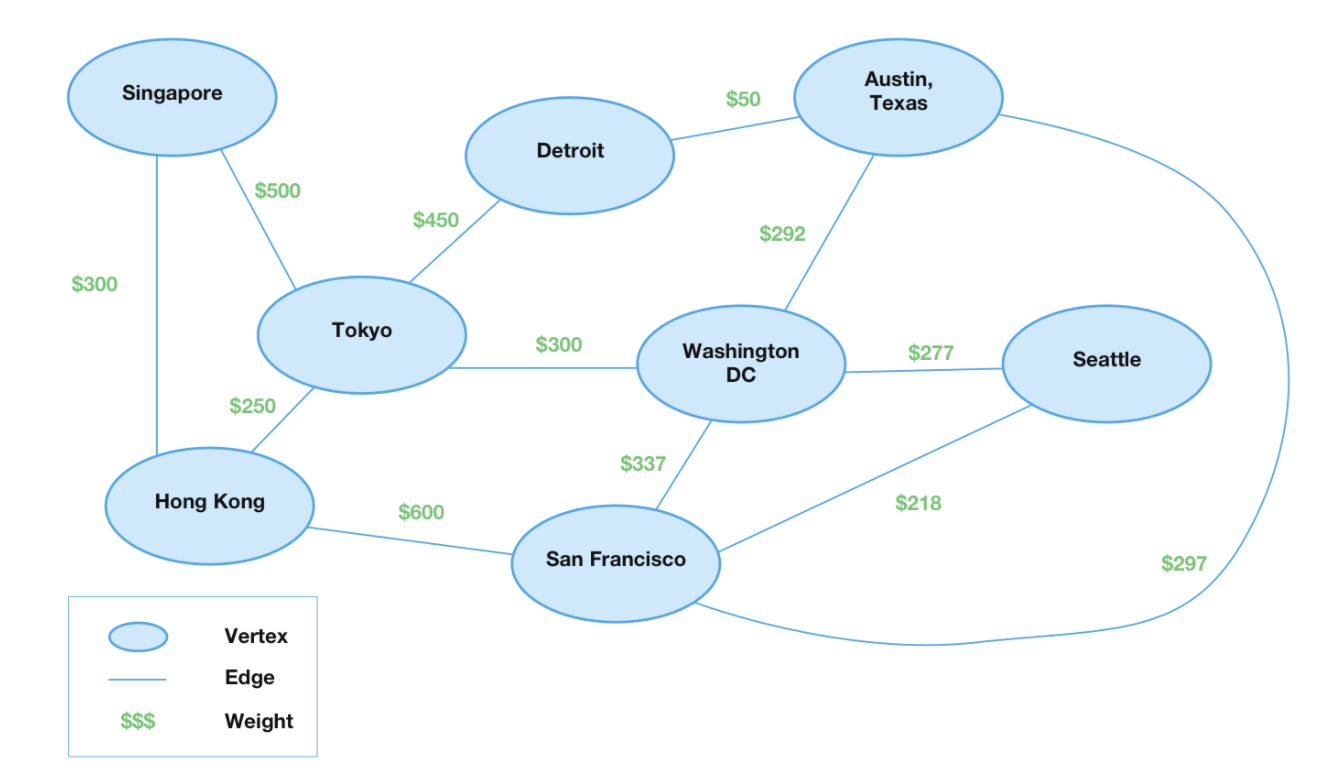

Figure 4

Figure 4 represents a labeled and weighted graph, where each edge has a numerical value indicating the price.

Labeled Graph

Weighted Graph

A weighted graph assigns numerical values to edges, often representing:

Applications of Graphs

(1) The Internet (Web Graph) The Internet, for example, is a vast, virtual graph. Every vertex is an individual webpage, and every edge means that there is a hyperlink between two pages.
Use Case: Google’s PageRank algorithm uses graphs to rank web pages. PageRank represents the web as a graph, where web pages act as nodes and hyperlinks function as edges. Web pages with more backlinks from high-quality sites receive higher rankings, helping Google Search display the most relevant results.

(2) Transportation Networks

Graphs also play an important role in transportation and navigation. All flight, train, and subway networks form graphs, which can be used when creating efficient schedules. One of the most recognisable graphs is the London Underground map:
Use Case: Google Maps, GPS navigation, and airline scheduling. Google Maps and GPS use graph-based algorithms to compute the fastest routes, considering traffic and distance. Airline scheduling relies on graph representations to optimize flight routes and minimize travel costs.

(3) Chemistry and Biology

The links between atoms in molecules and crystal grids form a graph.
Use Case: Used in drug discovery, protein structures, and genetics. Graphs play a crucial role in biomedical research by modeling molecular structures, predicting drug interactions, and aiding in drug development. They are also used to analyze protein interactions and genetic relationships, advancing disease research and personalized medicine.

(4) Social Networks

Use Case: Facebook, LinkedIn, Instagram use graphs to suggest new connections. Facebook, LinkedIn, and Instagram use graph algorithms to suggest new connections based on mutual friends, follower patterns, and shared interests. Machine learning and AI further refine these recommendations by analyzing user behavior for personalized suggestions.


Reference

saylor academy