Chapter 9: Finite-State Machines, Turing machines
Section 9.3 Finite-State Machines
Examples of Finite-State Machines
Finite-State Machines (FSMs) can be used for recognition — that is, to produce an output of 1 when the input matches a specific description.Recognition
A machine can be built to recognize , say by producing an output of 1, when the input it has received matches a certain description. We will soon discuss more fully the capabilities of finite-state machines as recognizers. Here we will simply construct some examples.
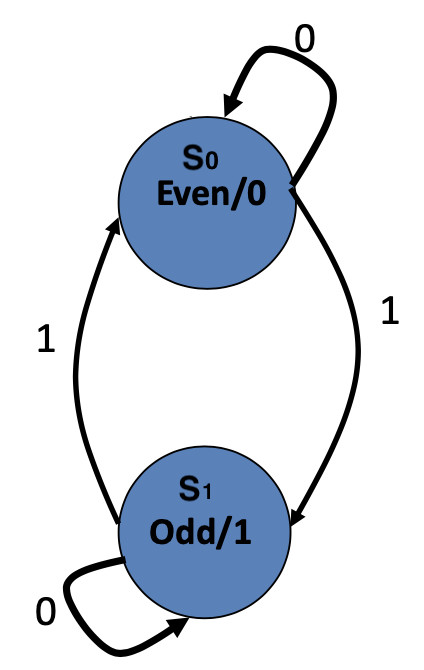
1. FSM for Even/Odd Parity Check:
Parity checker counts the number of 1's in a bit-serial input stream.
If the checker asserts its output when the input stream cotains an odd
number of 1's, it is called an
odd parity checker
.
If it asserts its output when it has seen an even number of 1's, it is an
even parity checker
.

| Present State | Next State | Output |
|---|---|---|
| Present Input 0 1 |
||
| \(S_0\) Even | \(S_0\) \(S_1\) | 0 |
| \(S_1\) Odd | \(S_1\) \(S_0\) | 1 |
Even(0), Odd(1):
We see that an input sequence consisting of the characters (0011101) would produce the output of 0:
| Time | \(t_0\) | \(t_1\) | \(t_2\) | \(t_3\) | \(t_4\) | \(t_5\) | \(t_6\) | \(t_7\) |
|---|---|---|---|---|---|---|---|---|
| Input | 0 | 0 | 1 | 1 | 1 | 0 | 1 | - |
| State | \(S_0\) | \(S_0\) | \(S_0\) | \(S_1\) | \(S_0\) | \(S_1\) | \(S_1\) | \(S_0\) |
| Output | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
Assuming an odd parity scheme, if the parity of the received string is not odd, then an error has occurred in transmitting the string, and a request for retransmission can be made. A parity bit therefore serves as a simple single-error-detection mechanism.
Practice
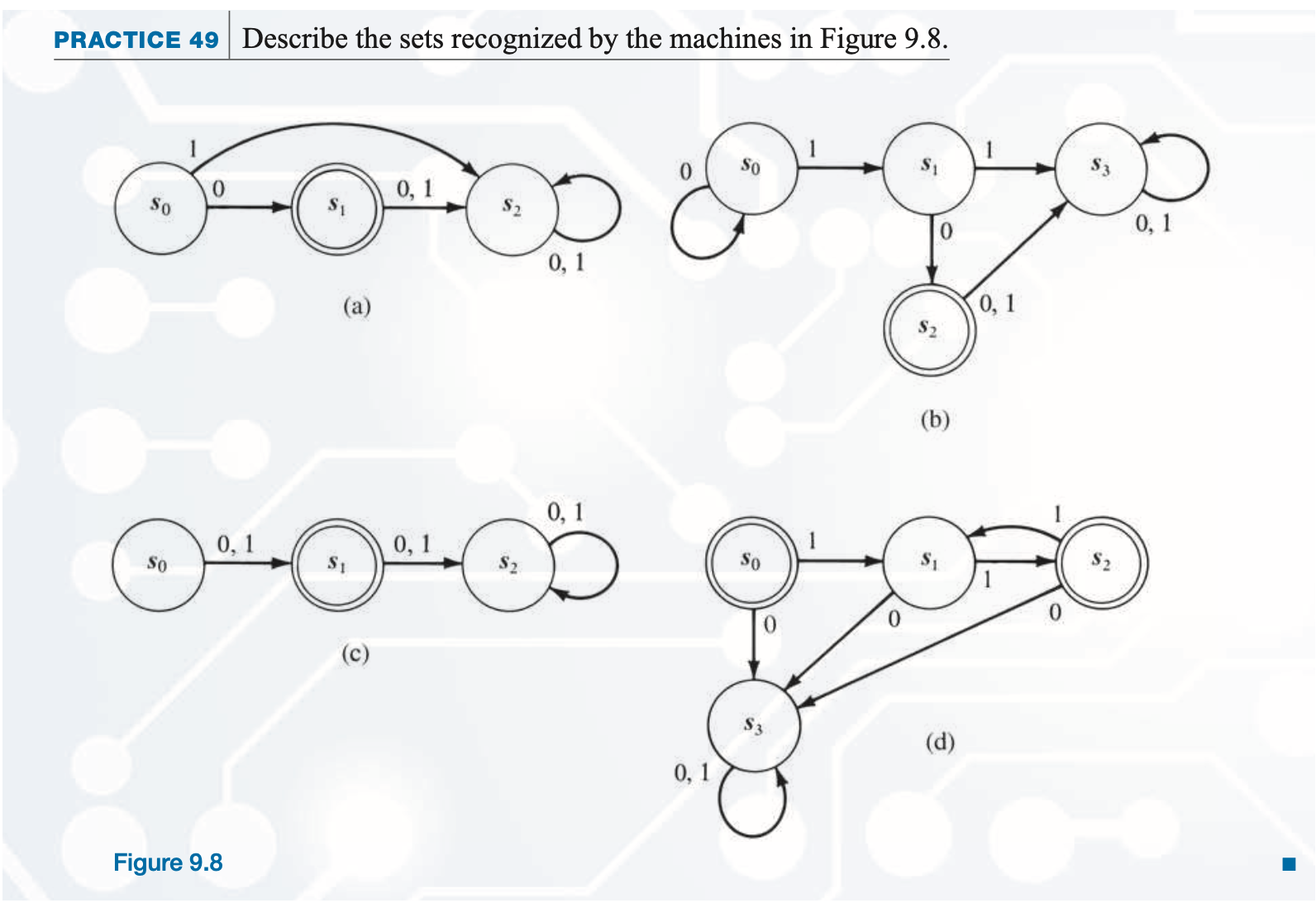
Redesign the odd parity checker FSM to make it check for even parity (that is, assert the output when the input contains an even number of 1's). Show your state table and state graph:
2. FSM for String Recognization
FSMs can also recognize whether a string matches a specific pattern.
What is this FSM trying to recognize?
The FSM is built to recognize if the last part of the input ends with "101".- If the string ends with "101", the machine outputs 1 (accept). (the machine has recognized the pattern "101")
- Otherwise, the output is 0 (reject). (the pattern "101" has not been found at the end of the string)
Explanation:
- ☆ Step 1: We use the target pattern (101) to build the basic states. To recognize 101, we need four states:
- ☆ The machine starts at state \(s_0 \).
- ☆ It moves between \(s_0, s_1,\) and \(s_2\) depending on the input (0 or 1).
- ☆ Only \(s_3 \)is a final (accepting) state.
- ☆ Only when the machine reaches \(s_3 \), it outputs 1 -- meaning it has detected the pattern "101" in the input.
- ☆ Otherwise, when the machine is in states \(s_0, s_1,\) or \(s_2\), the output remains 0. Because the full pattern "101" has not been recognized yet.
| State | Meaning |
|---|---|
| \(s_0\) (Start) | Nothing matched yet (starting point). |
| \(s_1\) | We have seen the first 1. |
| \(s_2\) | We have seen 10. |
| \(s_3\) (Final) | We have seen 101 (Accepting state, output = 1 ✅) |
- ☆ Step 2: Complete the transitions for every input at every state.
- ☆ For each state \( s_0, s_1, s_2, s_3\), you must decide where the machine should go next when the it reads: 1 or 0
- ☆ The examples 0101, 00101, or 000101 show that at state \(s_0\), if the input is 0, we should stay at \(s_0\). Since a 0 does not start the target pattern (101), the machine must remain at the start state and continue waiting for a 1.
- ☆ The examples 1101 and 11101 show that at state \(s_1\), if the input is 1, we should stay at \(s_1\). Since we are still seeing a sequence of 1's and have not yet matched the "10" part of the pattern, the machine should remain at \(s_1\) and keep waiting for a 0.
- ☆ The example 100101 shows that at state \(s_2\), if the input is 0, we should move back to \(s_0\). Since seeing another 0 after 10 means the pattern "101" has been broken, the machine must reset and start looking for a new potential match from the beginning.
- ☆ The example 10101 shows that at state \(s_3\), if the input is 0, we should move to \(s_2\). Since we just finished matching "101" and now see a 0, it matches the beginning of a new "10" pattern. Therefore, the machine should transition to s₂ to continue checking for another possible "101" sequence.
- ☆ The example 101101 shows that at state \(s_3\), if the input is 1, we should move to \(s_1\). Since we just finished matching "101" and now see a 1, it could be the start of a new "101" pattern. Therefore, the machine should transition to s₁ to begin tracking a new possible match.
Practice

Formal Definition
Now we want to see exactly what sets finite-state machines can recognize.To avoid writing down outputs, we will designate those states of a finite- state machine with an output of 1 as final states and denote them in the state graph with a double circle . Then we can give the following formal definition of recognition, where I* denotes the set of finite-length strings over the input alphabet.