Chapter 9: Finite-State Machines, Turing machines

Section 9.3 Finite-State Machines

Regular Sets and Kleene's Theorem

We want a compact, symbolic way to describe sets such as those appearing in the answer to Practice 49. We will describe such sets by using regular expressions ; each regular expression describes a particular set.

(Regular expressions, often abbreviated as regex or regexp, are sequences of characters that define a search pattern. They are used in various programming languages and text-processing tools to find and manipulate strings of text based on specific patterns. Regular expressions are a powerful tool for text processing and manipulation, but they can also be complex and difficult to understand at first. However, once you become familiar with their syntax and usage, they can greatly simplify many text-processing tasks.)



A Regular Set is a concept in automata theory and formal language theory. It refers to a set of strings that can be described or generated using a regular expression or recognized by a finite state machine. Regular sets represent the class of regular languages, which are the simplest types of languages in formal language theory.

• Φ (phi) represents the empty set — no strings at all.
• λ (lambda) Represents the empty string — the string with no characters.
• In formally, an element in AB is an item from A followed by an item from B. (Concatenation of two expressions)
• An element in \(A ∨ B\) is a single item chosen from either A or B. (Union (choice between A or B))
• An element in (A)* is zero or more repetitions of elements from A.
• We note that λ, the empty string, is a member of the set represented by A* for any A because it is the case of zero repetitions of elements from A. (A*: Zero or more repetitions of A)

The Kleene star operator (denoted by *) is a fundamental operation in formal language theory and regular expressions. It allows a pattern to be repeated zero or more times, effectively creating an infinite set of possible strings from a single base pattern.

In writing regular expressions, we can eliminate parentheses when there is no ambiguity results. The regular expression 0* ∨ 10 therefore consists of \(λ, 0, 00, 000, 0000, ..., 10.\)

We have introduced regular sets because, as it turns out, these are exactly the sets finite-state machines are capable of recognizing. This result was first proved by the American mathematician Stephen Kleene in 1956. We state his theorem here without proof.

Kleene's Theorem is a foundational result in automata theory and formal languages, formulated by mathematician Stephen Kleene. The theorem establishes an equivalence between regular expressions and finite automata, showing that they define the same class of languages, known as regular languages.

Kleene’s Theorem states that:

• If a set of strings (language) is recognized by a finite state machine, then it is a regular set, meaning it can be described by a regular expression..
• If a set of strings can be described by a regular expression, then there exists a finite state machine that recognizes it.

In general, regular expressions excel at describing linear, non-nested, repetitive patterns and simple structures that don’t require memory or context tracking, making them ideal for many text processing tasks but limited in handling more complex language structures.

Practice

(1) Please write regular expressions for the sets recognized by the finite-state machines of Practice 49: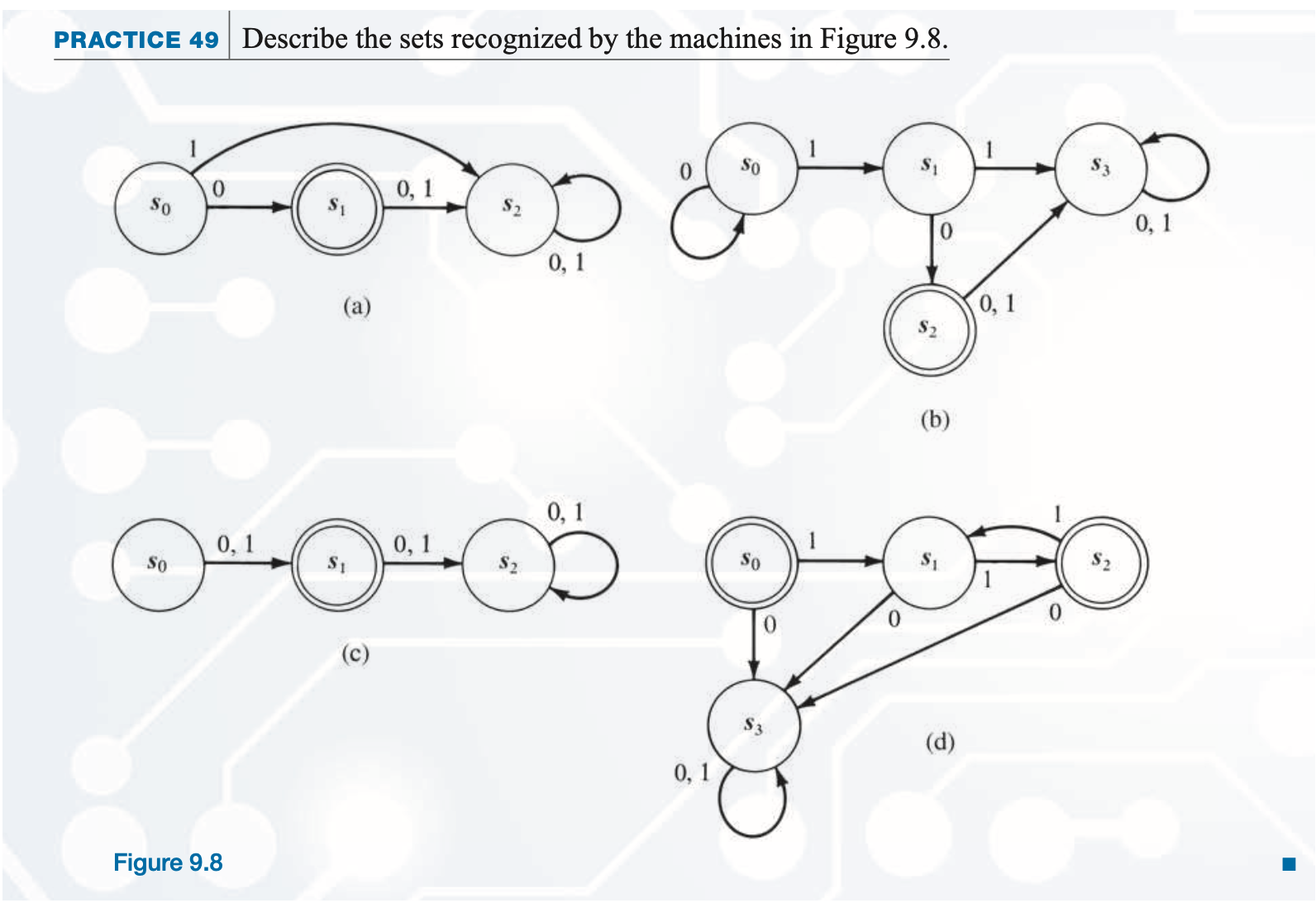

• (a) 0
• (b) 0*10
• (c) 0 \( ∨ \) 1
• (d) (11)*

Reference

Wikipedia