Chapter 9: Finite-State Machines, Turing machines
Section 9.3 Finite-State Machines
finite-state machine (FSM) or finite-state automaton (FSA, plural: automata), finite automaton, or simply a state machine, is a mathematical model of computation .A finite state machine is a mathematical abstraction used to design algorithms. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition . An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition.
A finite-state machine (FSM) is an abstract computational model used to design and describe systems with a finite number of states. It's a mathematical model that consists of a finite number of states, a set of inputs, a set of outputs, and a set of transitions between states based on inputs. FSMs are widely used in various fields such as computer science, engineering, and mathematics to model and control systems that have a finite number of states. FSMs are fundamental in understanding and designing systems with discrete states and transitions.
Finite state automata generate regular languages. Finite-state machines can be used to model problems in many fields including mathematics, artificial intelligence, games, and linguistics. parking meter, pop machine, automated gas pump, and all kinds of other things.
Example: coin-operated turnstile
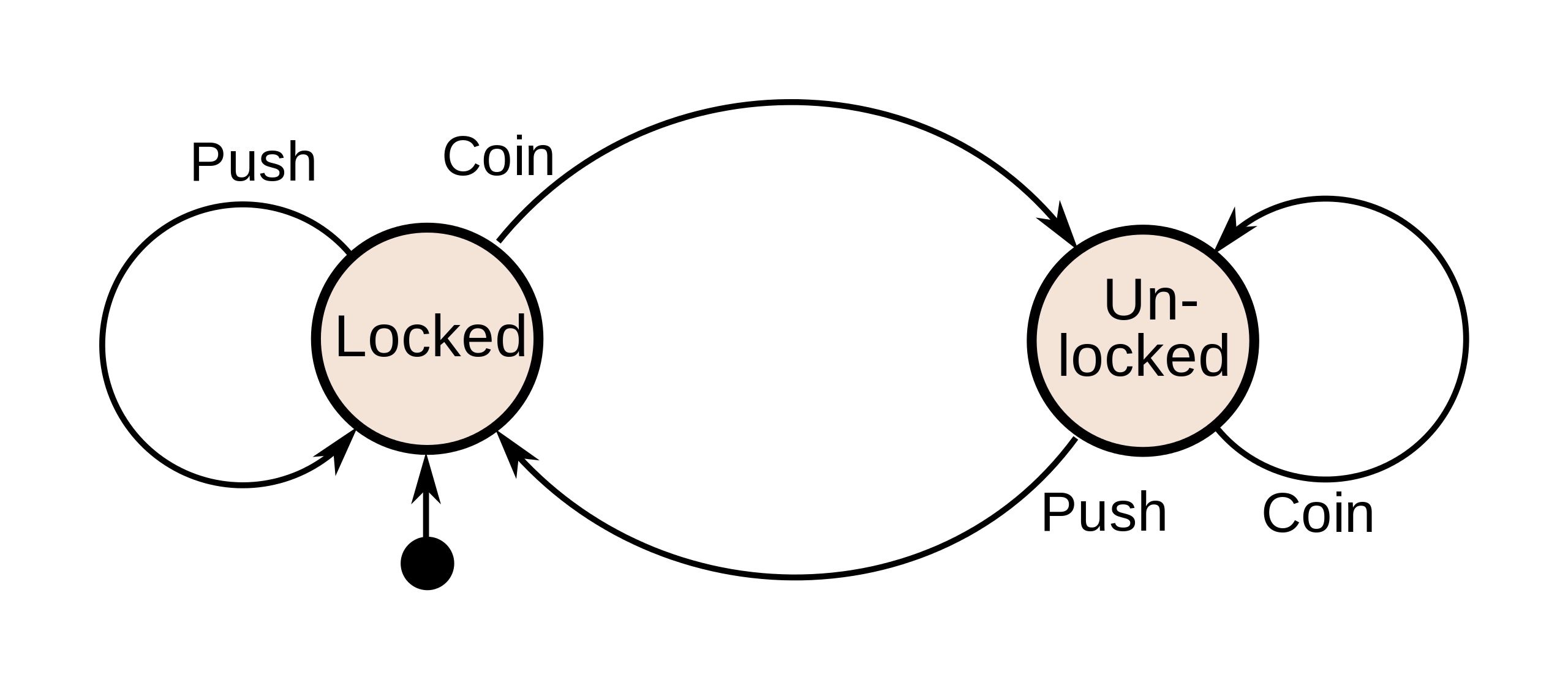
The turnstile state machine can be represented by a state-transition table, showing for each possible state, the transitions between them (based upon the inputs given to the machine) and the outputs resulting from each input:

Formal Definition

Examples of Finite-State Machines
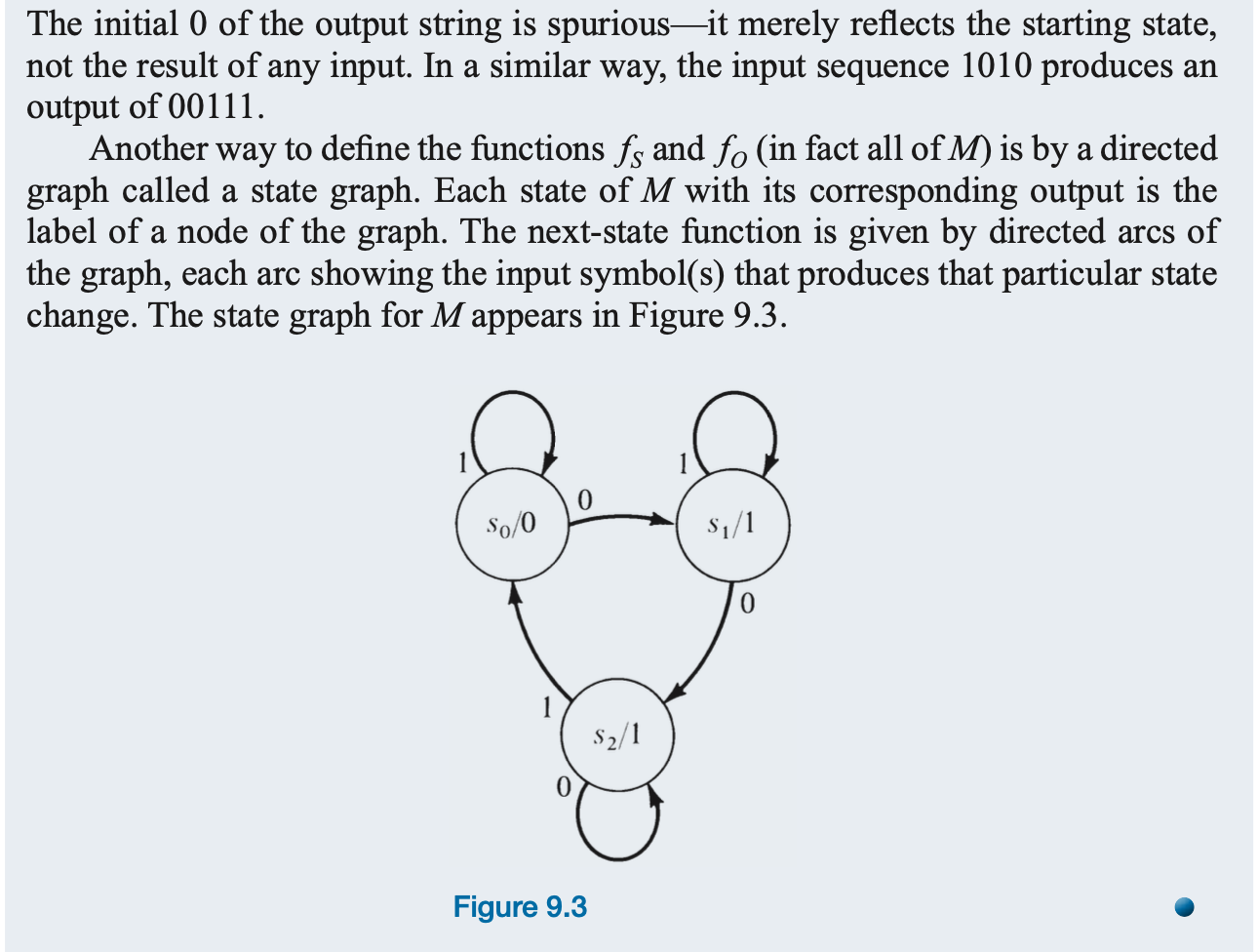
To describe a particular finite-state machine, we have to define the three sets and two functions involved.Example 29:

FSM Examples in Daily Live
- Vending Machines
- Traffic Lights
- Elevators
- Alarm Clock
- Microwave
- Cash Registers
- Lexical Analysis in Compilers
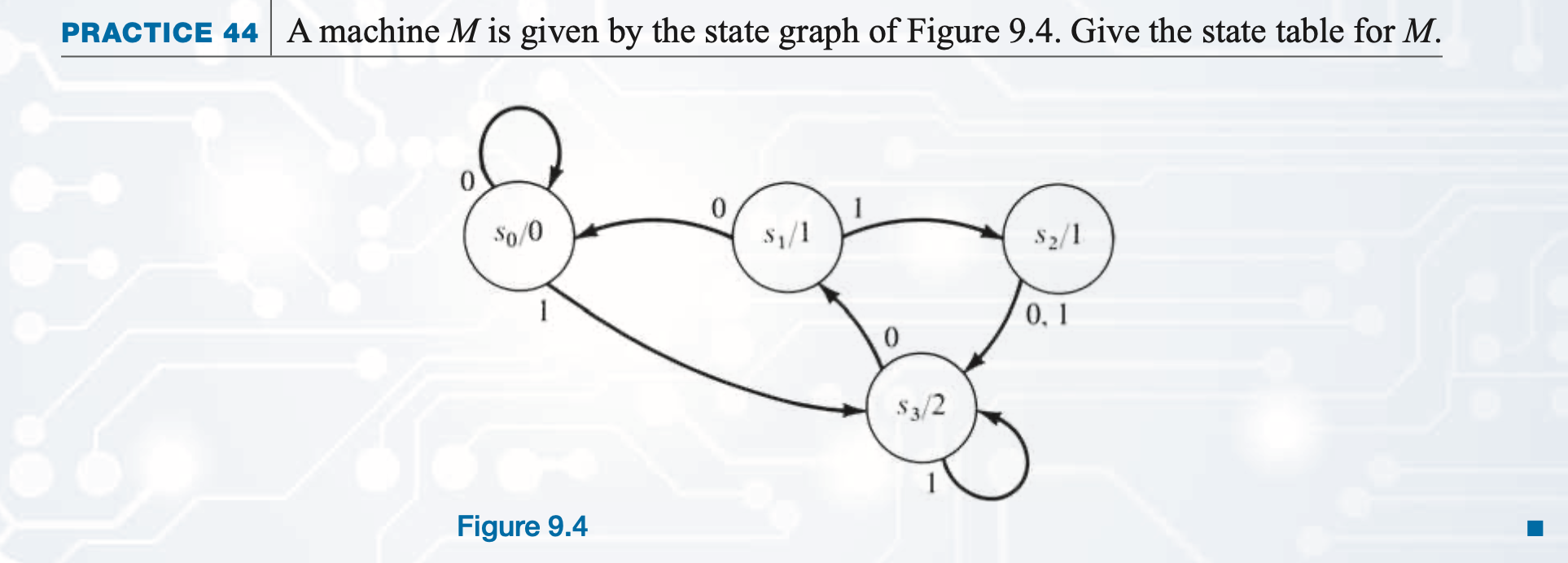
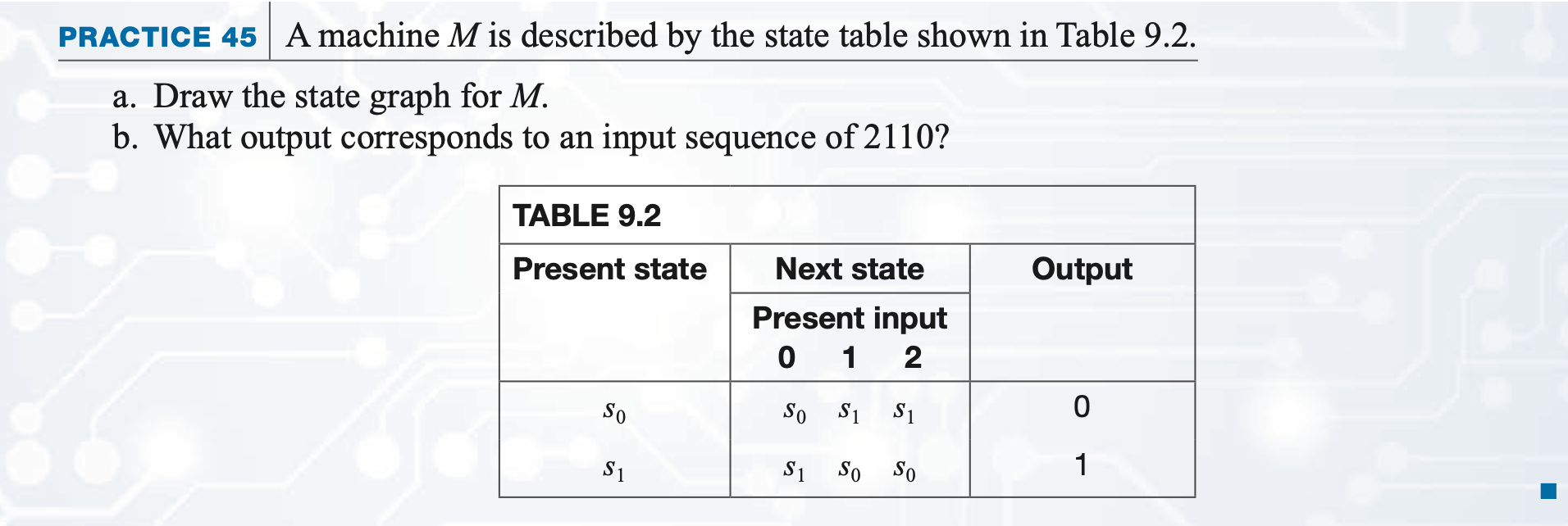
Practice
Who invented Finite-State Machines (FSM)?
The concept of Finite-State Machines (FSM) was developed by several important researchers:- 1. Warren McCulloch and Walter Pitts (1943) ☆ They created the first idea similar to FSMs to model how neurons work in our brains.
- 2. George H. Mealy and Edward F. Moore (1950s) ☆ They independently developed formal FSM models:
- ♣ Mealy Machine (1955): Output depends on the current state and input.
- ♣ Moore Machine (1956): Output depends only on the current state.
- 3. Michael O. Rabin and Dana Scott (1959) ☆ They formally defined FSMs (called Finite Automata) mathematically, greatly influencing computer science.
☆ Theoretical Foundations: Introduced the concept formally as Finite Automata in their paper "Finite Automata and Their Decision Problems."
☆ They received the Turing Award (the "Nobel Prize" of computer science) for this work in 1976.
Reference
WikipediaBrilliant