Chapter 9: Finite-State Machines, Turing Machines
Section 9.5 Formal Languages
Languages derived from grammars such as we have defined are called formal languages . If the grammar is defined first, the language will follow as an outcome of the definition.


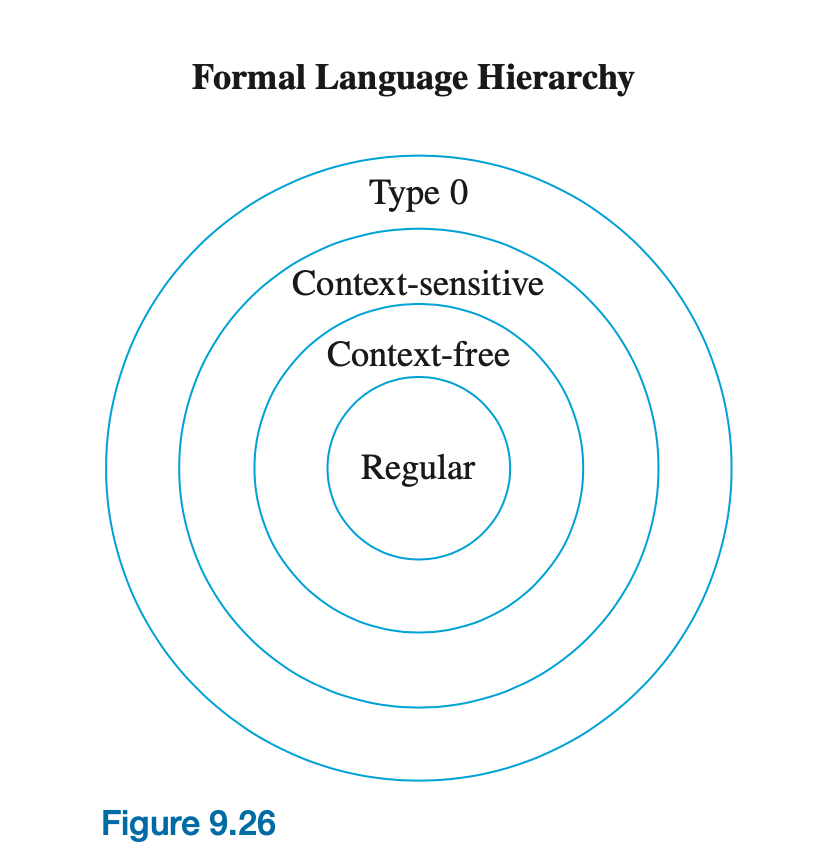
The hierarchy consists of four levels of grammars, each capable of generating increasingly complex sets of languages:
- Type 0 – Recursively Enumerable Languages (Unrestricted Grammar)
- Type 1 – Context-Sensitive Languages (Context-Sensitive Grammar)
- Type 2 – Context-Free Languages (Context-Free Grammar)
- Type 3 – Regular Languages (Regular Grammar)
Formal Languages and Computational Devices
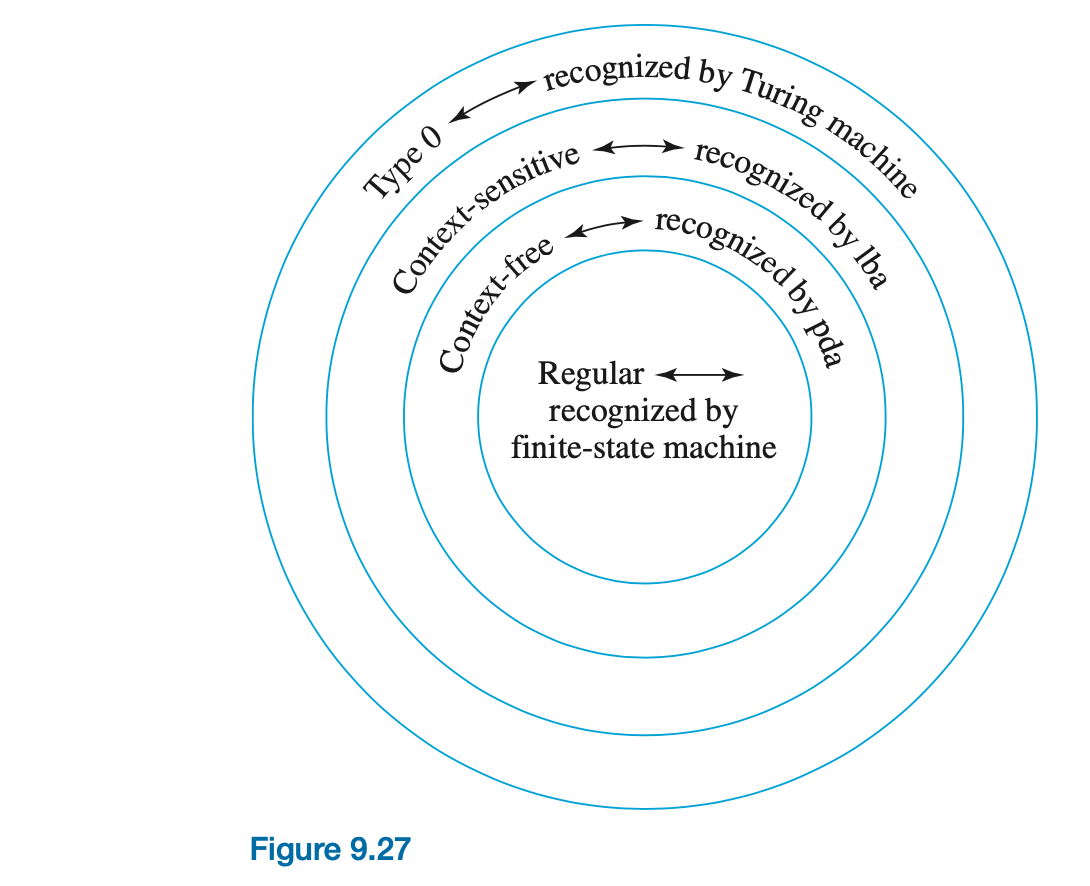
The class of sets recognized by a computational device of limited capacity coincides with the most restricted class of languages. The most general computational device is the Turing machine and the most general language is a type 0 language. As it happens, the sets recognized by Turing machines correspond to type 0 languages.There are computational devices with capabilities midway between those of finite-state machines and those of Turing machines. These devices recognize exactly the context-free languages and the context-sensitive languages, respectively.
The type of device that recognizes context-free languages is called a pushdown automaton , or pda . A pda consists of a finite-state unit that reads input from a tape and controls activity in a stack. Symbols from some alphabet can be pushed onto or popped off of the top of the stack. The finite-state unit in a pda, as a function of the input symbol read, the present state, and the top symbol on the stack, has a finite number of possible next moves. It can be shown that any set recognized by a pda is a context-free language, and conversely.
The type of device that recognizes the context-sensitive languages is called a lba . lba stands for "Linear Bounded Automaton". An lba is a Turing machine whose read-write head is restricted to a portion of the tape that is no longer than a constant multiple of the length of the original input; in addition, at each step it has a choice of possible next moves. An lba recognizes the set of all inputs for which some sequence of moves exists that causes it to halt in a final state. Any set recognized by an lba can be shown to be a context-sensitive language, and conversely.
Figure 9.27 shows the relationship between the hierarchy of languages and the hierarchy of computational devices.
Formal Languages
Regular Language:
A regular language is like a simple language that follows a set of easy-to-understand rules. Imagine you have a magic toy that only allows you to press certain buttons in a specific order to make it work. The toy will do different things depending on the buttons you press. A regular language is like a set of rules that tells you which buttons you can press and in what order to make the toy work. It's simple and easy to understand because the rules are straightforward and don't have any complicated conditions.Context-Free Language:
A context-free language is like a language that has a few more rules than a regular language. Imagine you're playing with a set of building blocks, and you have a set of instructions that tell you how to stack the blocks. The instructions might say things like "put a green block on top of a red block" or "put a blue block next to a yellow block." These instructions give you more flexibility in how you can stack the blocks, but they still have some limitations. A context-free language is like a set of rules that tell you how to arrange words or symbols in a sentence. The rules allow you to combine words in different ways, but they still have some restrictions.Context-Sensitive Language:
A context-sensitive language is like a language with even more rules and flexibility. Imagine you have a storytelling game where you can create your own adventure. In this game, you can add characters, locations, and events to the story, and you can even change the rules of the game as you go. A context-sensitive language is like a set of rules that give you a lot of freedom to create your own story. You can add new characters, change the order of events, and modify the rules of the game, as long as everything still makes sense within the context of the story.Type 0 Language:
Type 0 languages are the most powerful and flexible type of language. They can describe any kind of language, no matter how complex. Imagine you have a magic pen that can write any word or sentence you imagine. With this pen, you can write stories, poems, or even create your own language. Type 0 languages allow you to define your own rules and create new words and sentences that have never been seen before.To summarize, regular languages have simple and straightforward rules, context-free languages have more flexibility but still have some restrictions, context-sensitive languages give you even more freedom to create your own rules, and type 0 languages allow you to define your own rules and create new words and sentences.
Computational Devices and Language Recognition
| Device | Memory | Recognizes | Examples Recognized | Limitations |
|---|---|---|---|---|
| Finite State Machine (FSM) | Finite number of states | Regular Languages | Simple patterns like "strings ending with ab", email format checking | Cannot count matching numbers (cannot handle aⁿbⁿ). |
| Pushdown Automaton (PDA) | Stack (LIFO) | Context-Free Languages | Balanced parentheses, syntax checking in programming languages | Cannot handle multiple dependencies (cannot do aⁿbⁿcⁿ). |
| Linear Bounded Automaton (LBA) | Fixed tape size (bounded by input length) | Context-Sensitive Languages | Matching equal numbers of a’s, b’s, and c’s (aⁿbⁿcⁿ) | Cannot recognize languages more complex than context-sensitive. |
| Turing Machine (TM) | Infinite tape | Recursively Enumerable Languages | All computable problems; including ones without guaranteed halting | Some problems are undecidable — no algorithm can always solve them. |
Reference
saylor academyBrilliant
Stanford Encyclopedia of Philosophy