Chapter 7: Graph Algorithms
Section 7.2 Euler Path and Hamiltonian Circuit
An Euler Path (or Eulerian Path) is a path in a graph that visits every edge exactly once. It is named after the mathematician Leonhard Euler, who first solved the famous Seven Bridges of Königsberg problem, which led to the foundation of graph theory.
📘 Famous Origin: The Seven Bridges of Königsberg
Leonhard Euler was trying to solve:
Is it possible to walk through the city and cross each of the seven bridges once without repeating any?
🧠 Euler proved that it wasn’t possible, and this led to the birth of graph theory!
Euler Path
An Euler path in a graph G is a path that uses each arc of G exactly once.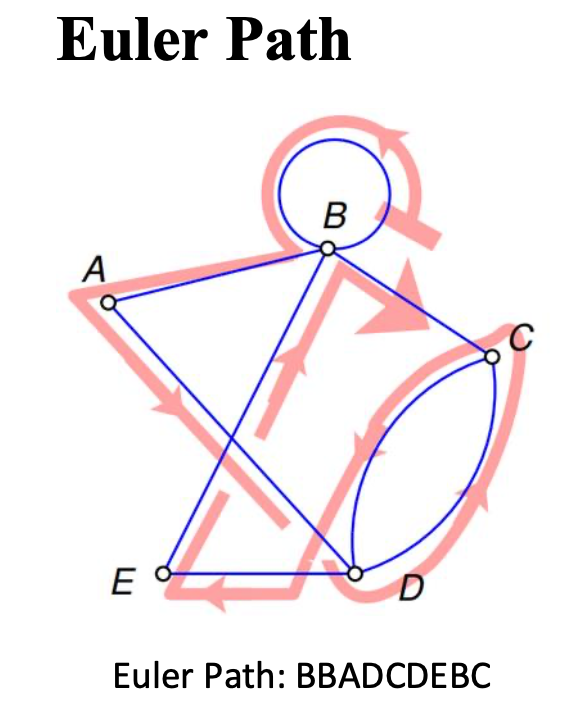
Key Characteristics of Euler Path:
- Directed and Undirected Graphs: Euler paths can be found in both directed and undirected graphs.
- Every Edge Once: The key feature of an Euler path is that every edge must be visited exactly once, but vertices can be visited more than once.
- An Euler path exists in a graph if there are zero or two odd nodes.
Euler's Theorem for Undirected Graph
What does Even Node and Odd Node mean?
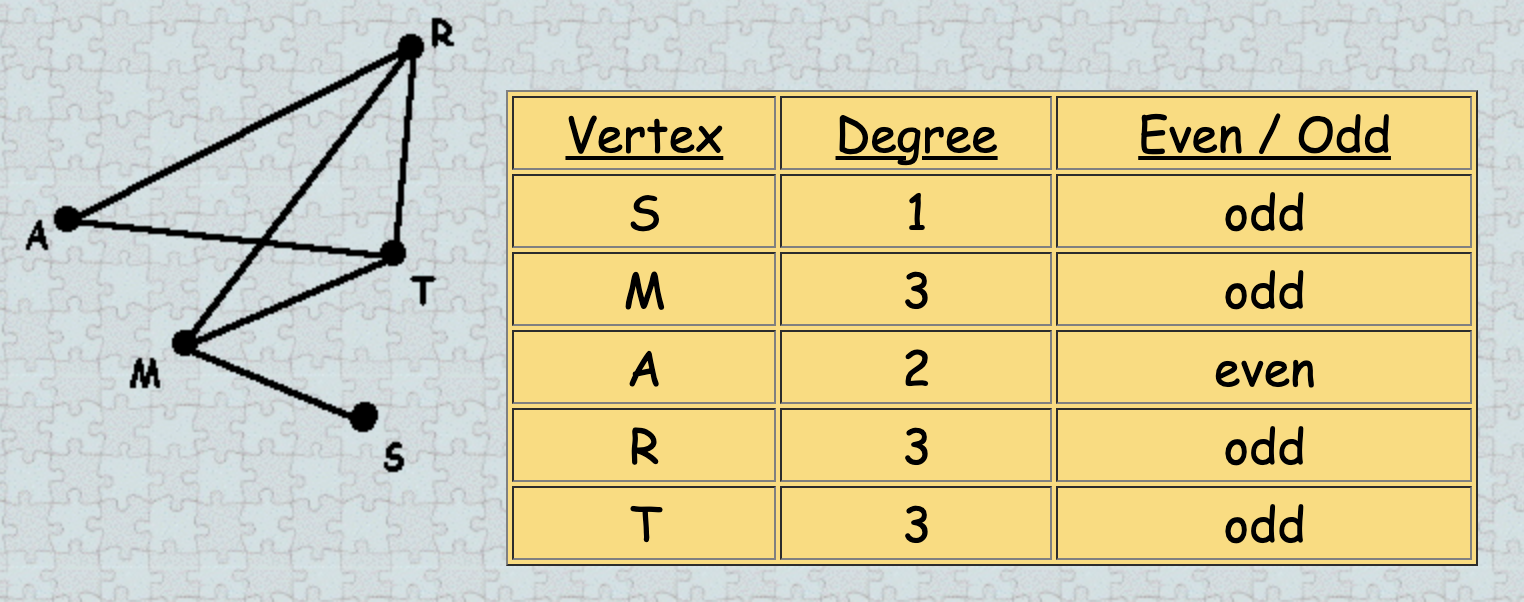
1. The number of odd nodes in any graph is even.
2. An Euler path exists in a graph if there are zero or two odd nodes.
If there are zero odd node, then the euler path can begin at any node and will end at the same node. (Euler Circuit: closed path)
If there are two odd nodes, the euler path will begin at one odd node and end at the other odd node.
3. If a graph has more than 2 odd nodes, then it has no Euler paths.
| #Odd Vertices | Euler Path? |
|---|---|
| 0 | Yes (Euler Circuit) |
| 2 | Yes |
| 4,6,8 ... | NO |
| 1,3,5 ... | No Such Graphs Exist!!! |
Example
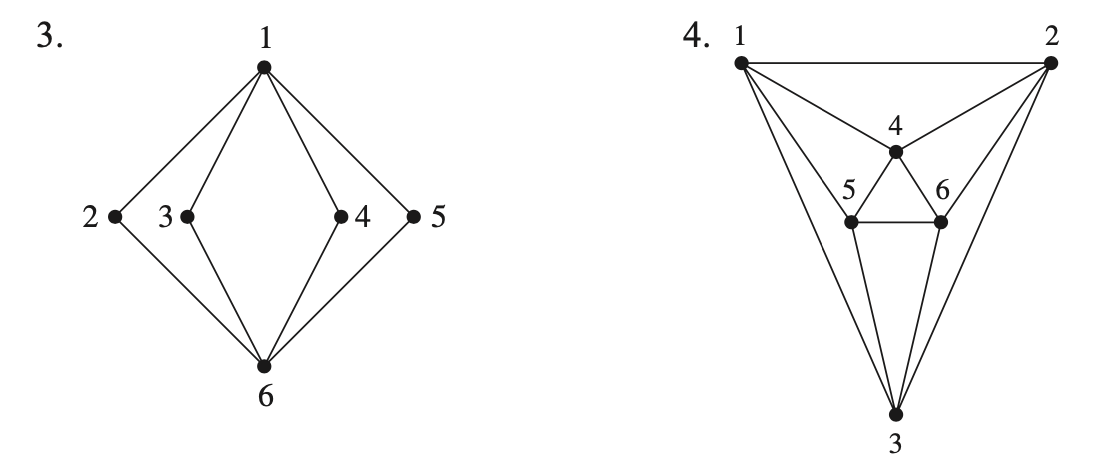
3. There are zero odd nodes. Yes, it has euler path. (eg: 1,2,6,3,1,4,6,5,1)
4. There are zero odd nodes. Yes, it has euler path. (eg: 1,2,4,1,5,4,6,2,3,6,5,3,1)
Note:
- ★ For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices. A special case is a loop , which adds two to the degree.
- ★ For a directed graph, a loop adds one to the in degree and one to the out-degree.
Hamiltonian Circuit
A Hamiltonian Circuit (or Hamiltonian Cycle) is a closed loop in a graph that visits each vertex exactly once and returns to the starting vertex. In contrast to an Euler Path, which visits every edge once, a Hamiltonian Circuit focuses on visiting every vertex once without revisiting any of them, except for the return to the starting point.Key Characteristics of a Hamiltonian Circuit:
- Visits Every Vertex: The circuit includes every vertex in the graph.
- No Repeated Vertices: Each vertex is visited exactly once, except for the starting vertex, which is visited again at the end to complete the circuit.
- Closed Path: The path ends where it started.
A Hamiltonian circuit in a graph is a cycle using every node of the graph. A Hamiltonian circuit is a circuit that visits every vertex once with no repeats.
No efficient algorithm has ever been found to determine if a Hamiltonian circuit exists.
Hamiltonian circuit problem can be solved for a given graph by trial and error. The algorithm is as follows: Start from one node of the graph and try some paths by choosing various arcs. If the path results in a repeated node, it is not a cycle, so throw it away and try a different path. If the path can be completed as a cycle, then see whether it visited every node; if not, throw it away and try a different path. Continue in this fashion until all possible paths have been tried or a Hamiltonian circuit has been found. The trial-and-error approach is theoretically possible, but it is practically impossible! In all but the smallest of graphs, there will simply be too many paths to try.
Finding a Hamiltonian Circuit can be more complex than finding an Eulerian path, as there is no simple criterion (like degree conditions for Eulerian paths) that guarantees the existence of a Hamiltonian Circuit. The Hamiltonian Circuit Problem is an NP-complete problem, meaning it is computationally challenging to solve, especially for large graphs.
Example

3. No, it has no Hamiltonian circuit.
4. Yes, it has Hamiltonian circuit. (eg: 1,4,2,6,3,5,1)
🎯 Euler Path vs. Hamiltonian Circuit: Summary Chart
| Feature | Euler Path | Hamiltonian Circuit |
|---|---|---|
| Visits every... | Edge exactly once | Vertex exactly once |
| Simple condition? | ✅ Yes (degree rules) | ❌ No |
| Easy to check? | ✅ Yes | ❌ No |
| Efficient algorithm? | ✅ Yes | ❌ No |
| NP-Complete? | ❌ No | ✅ Yes |
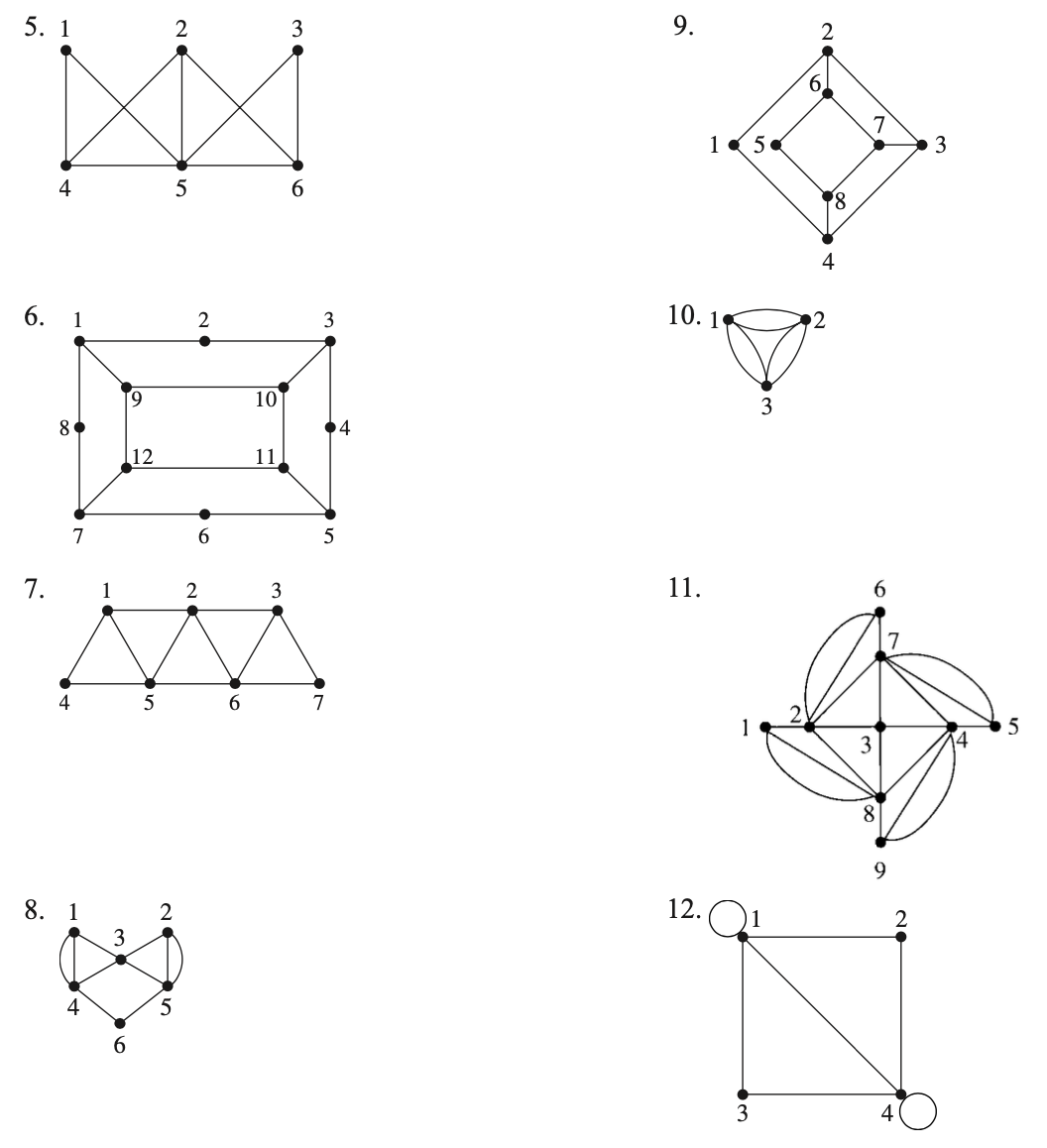
Practice
1. Do the following graph have Euler path?2. Do the following graph have Hamiltonian circuit?
Euler Paths give us the theoretical foundation for solving routing problems like:
- ☆ Street sweeping
- ☆ Garbage pickup
- ☆ Mail/postal delivery
- ☆ Utility inspections
- ☆ Snow plowing
Hamiltonian Circuits give us the theoretical foundation for solving visit-every-location-once problems like:
- ☆ Traveling sales routes
- ☆ Delivery driver planning
- ☆ School bus routing
- ☆ Drone flight paths
- ☆ Circuit board design