Chapter 7: Graph Algorithms

Section 7.4 Traversal Algorithms

In this section we deal with a simpler problem--we only want to write down all the nodes of a simple, connected graph G in some orderly way. This means we must find a path that visits each node at least once, but we can visit it more than once if we don't write it down again. We can also retrace arcs on the graph if necessary, and clearly this would in general be necessary if we were to visit each node in a tree. This process is called graph traversal . We already have several mechanisms for tree traversal (Section 6.2). The two algorithms in this section generalize traversal to apply to any simple, connected graph.

Depth-First Search (DFS)

• ☆ DFS is a graph traversal algorithm that explores as deep as possible along each branch before backtracking.
• ☆ It starts at a selected node, visits an unvisited neighbor, and keeps going deeper until it reaches a dead end—then it backtracks and tries other paths.
• ☆ DFS can be implemented using recursion or a stack.

In the depth-first search algorithm for graph traversal, we begin at an arbitrary node a of the graph, mark it visited, and write it down. We then strike out on a path away from a, visiting and writing down nodes, proceeding as far as pos- sible until there are no more unvisited nodes on that path. We then back up the path, at each node exploring any new side paths, until finally we retreat back to a. We then explore any new paths remaining from a. Figure 7.13 shows a graph after the first few nodes (marked by circles) have been visited using depth-first search.

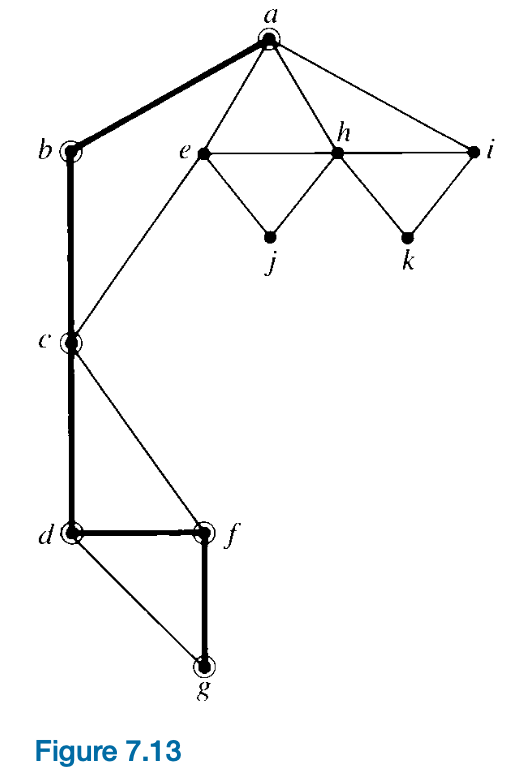
For a more formal description of the depth-first search algorithm we will use recursion, where the algorithm invokes itself in the course of its execution. In the following algorithm, the input is a simple, connected graph G and a specified node a; the output is a list of all nodes in G in depth-first order from a.

In the recursive step, the algorithm is invoked with a new node specified as the starting point.

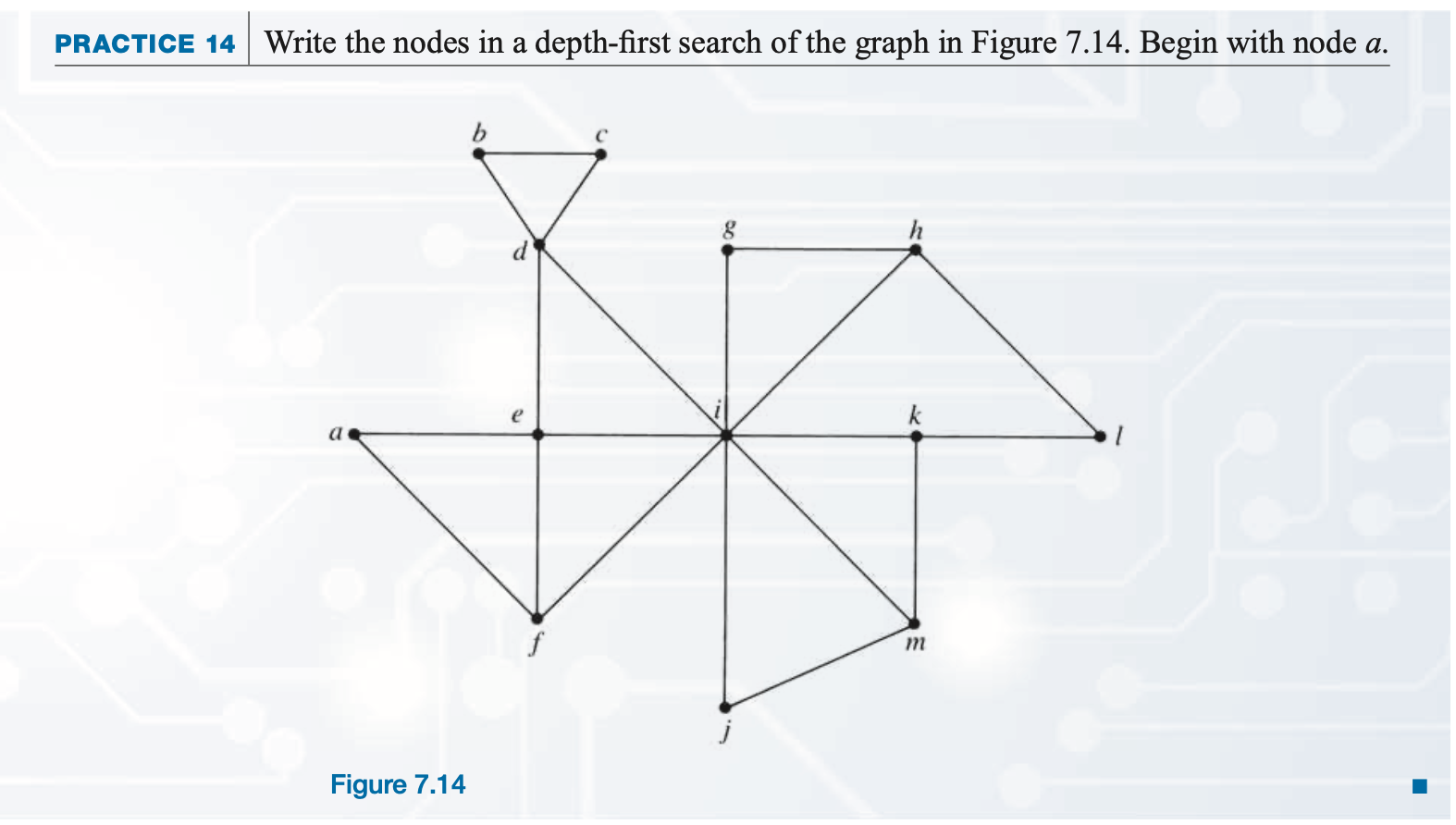
Practice

Recursive DFS Sudoku Solver (JavaScript version)

Recursive DFS Sudoku Solver

Reference

saylor academy