Chapter 6: Graphs and Trees

Section 6.3 Decision Trees

We learn decision trees when studying the lower bound of searching and sorting because they provide a visual and theoretical framework to understand the minimum number of comparisons required to solve these problems.

Decision Tree

A decision tree is a tree-like structure used to model decision-making processes, where the internal nodes represent actions, the arcs represent outcomes of an action and the leaves represent final outcomes. It's particularly useful for visualizing and understanding the steps an algorithm follows to reach a conclusion.

Sometimes useful information can be obtained by using a decision tree to represent the activities of a real algorithm; actions that the algorithm performs take place at internal nodes, the children of an internal node represent the next action taken, based on the outcome of the previous action, and the leaves represent some sort of circumstance that can be inferred upon algorithm termination.

Decision Tree in Search Algorithms

In the context of search algorithms, a decision tree helps us understand the number of steps (comparisons) required to find an element or determine that it’s not present in a list.

We learn decision trees in search algorithms to:

♣ Visualize how decisions branch out.
♣ Model the search space (e.g., every possible action and state).
♣ Understand efficiency (e.g., why binary search takes \(log_2(n)\) decisions).

Searching

A search algorithm either finds a target element x within a list of elements or determines that x is not in the list. Such an algorithm generally works by making successive comparisons of x to the list items. We have already seen two such algorithms, sequential search and binary search .We can model the activities of these algorithms by using decision trees.The nodes represent the actions of comparing x to the list items, where the comparison of x to the ith element in the list is denoted by x:L[i].

1. Sequential Search (also called Linear Search)

In sequential search, the algorithm compares the target element \(x\) with each element in the list one by one, starting from the first element.
If \(x=L[i]\), the target is found, the search ends.
If \(x!=L[i]\), the search moves to the next element \(L[i+1]\).
The decision tree for sequential search is linear, with each comparison leading directly to the next. The worst-case scenario, where the target element is not in the list, requires \(n\) comparisons for a list of \(n\)elements. The depth of the tree is therefore \(n\), as every node represents one comparison.

Sequential search only distinguishes between two possible outcomes of a comparison of x to L[i]. If x = L[i], the algorithm terminates because x has been found in the list. If x != L[i], the next comparison performed is x:L[i+1], regardless of whether x was less than or greater than L[i]. The leaves of this decision tree correspond to the final outcomes, where either x is one of the list items or x is not in the list.

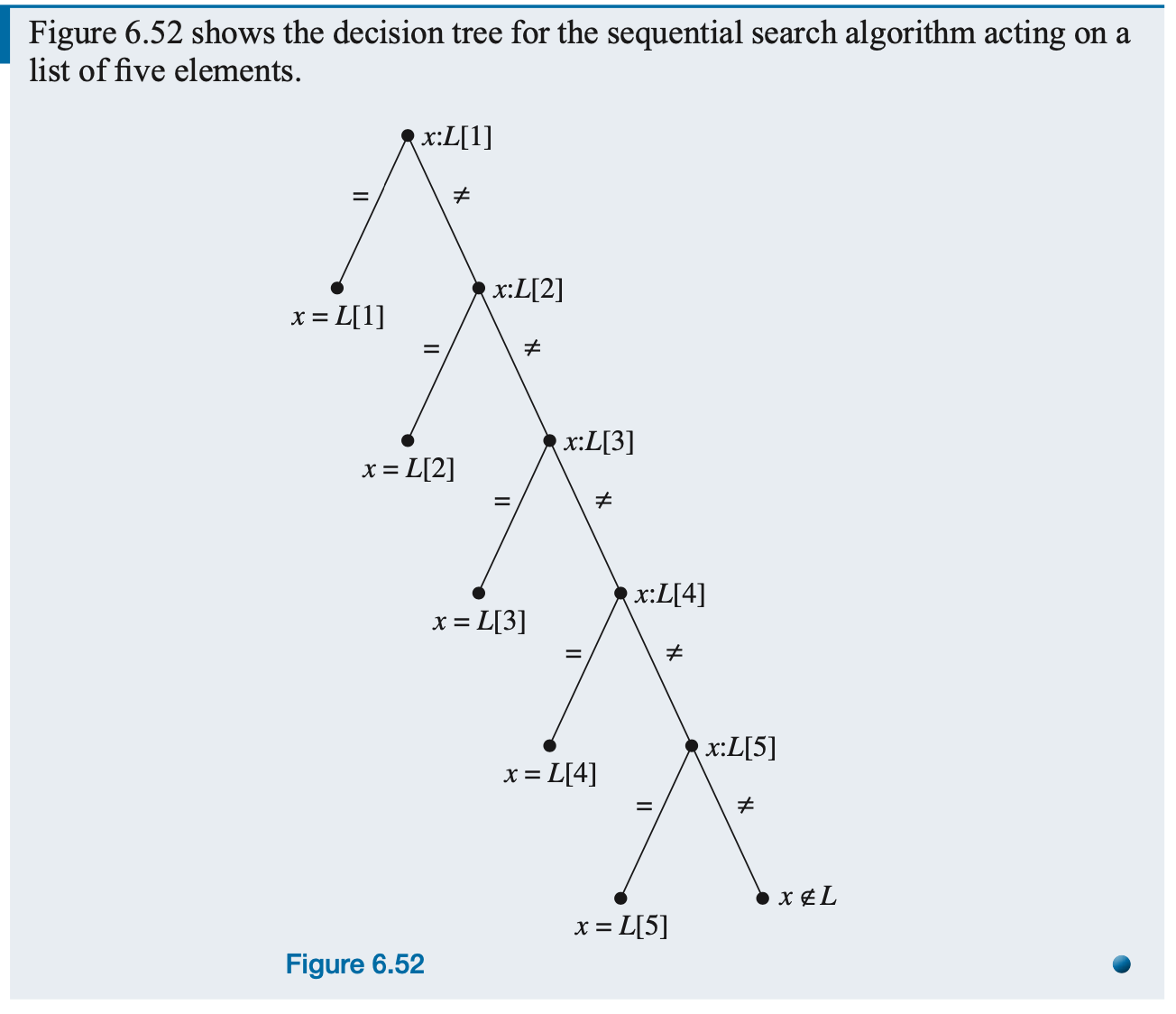
From the decision tree for a given search algorithm, we can see that the number of comparisons required to reach any particular outcome (leaf of the tree) is the number of internal nodes from the root to that leaf. This number equals the length of the path from the root to that leaf. The worst case, that is, the maximum number of comparisons, is the maximum length of any such path, which is the depth of the tree.

Because every decision tree for sequential search looks like Figure 6.52, it is clear that the depth of such a tree, for an n-element list, is n. This agrees with what we already know, namely, that the worst case for sequential search on a list of n elements is n.

Linear Search Demo

2. Binary Search

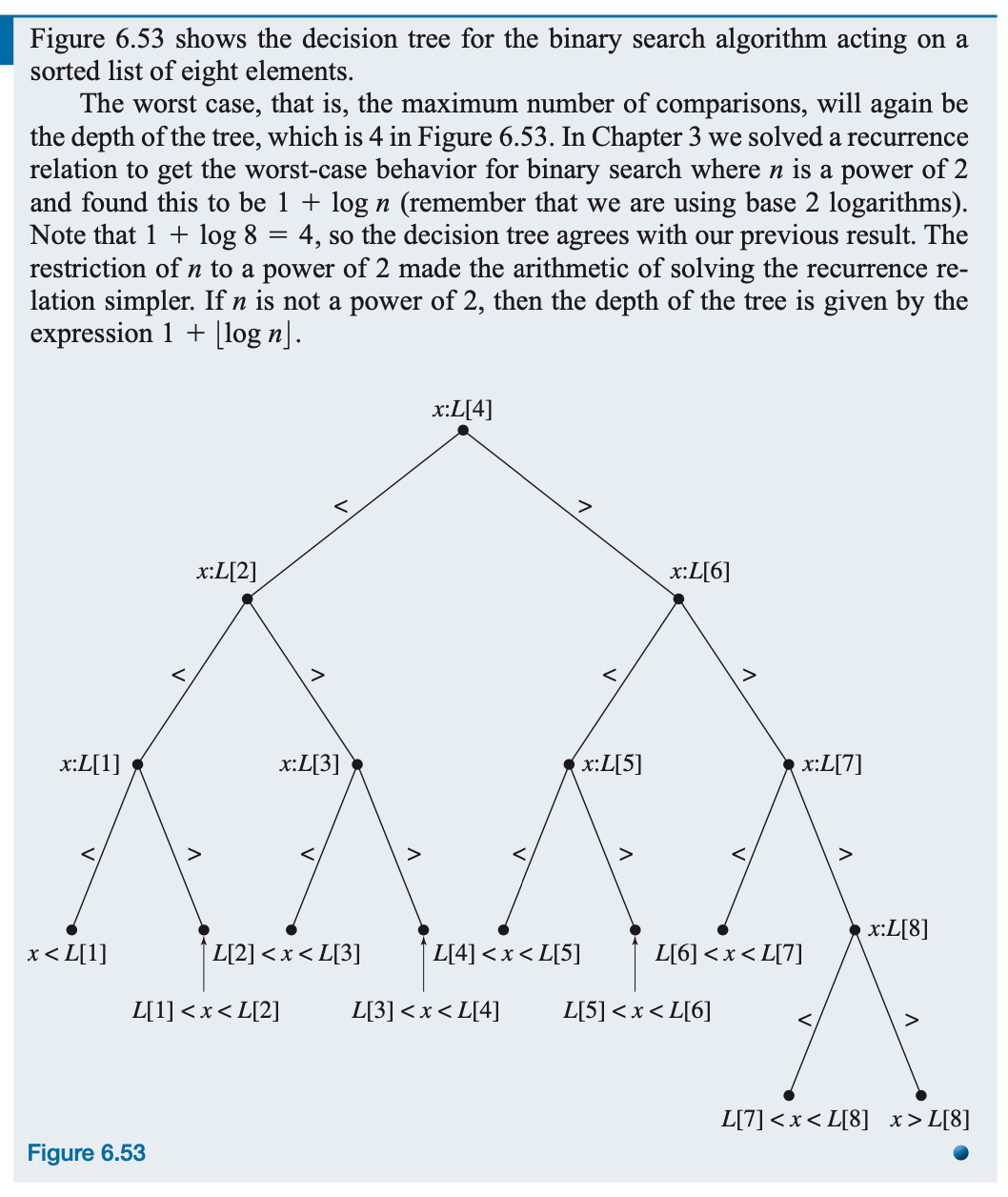
The decision tree for the binary search algorithm is more interesting. Binary search acts on a sorted list and distinguishes between three possible outcomes of the comparison:

x = L[i]: algorithm terminates, x has been found
x < L[i]: algorithm proceeds to the left half of the list 
x > L[i]: algorithm proceeds to the right half of the list

If x < L[i], the next comparison the algorithm performs is found at the left child of this node; if x> L[i], the algorithm's next comparison is found at the right child. If no child exists, the algorithm terminates because x is not in the list. The tree we've described is a binary tree whose leaves represent all the possible outcomes where x is not in the list. There are many more failure leaves in binary search than in sequential search, because binary search indicates how x fails to be in the list (e.g., x < L[1] or L[1] < x < L[2]).

The decision tree for binary search is a binary tree, where each comparison divides the list into two parts. The depth of the tree is \(log_2(n)\), making it much shallower than that of the sequential search. The worst-case scenario requires only \(log_2(n)\) comparisons.

Binary Search Demo

Practice

Sequential Search vs Binary Search

Feature	Sequential Search	Binary Search
Search method	Checks elements one by one	Divides the list in half each time
Time Complexity (Best Case)	O(1) (first element is the target)	O(1) (middle element is the target)
Time Complexity (Worst Case)	O(n): The worst case happens when: - The target is at the last position. - Or the target is not in the array at all. In both cases, the algorithm checks all n elements.	O(log n): The worst case happens when: - The target is not in the array. - Or the target is located at the final step after repeatedly halving the list. In both cases, the algorithm performs approximately \(log_2(n)\) steps.
Time Complexity (Average Case)	O(n): On average, linear search will check about half of the elements (n/2), but in Big-O we simplify it to O(n).	O(log n): On average, binary search will divide the list about \(log_2(n)\) times to find the target due to halving the list at each step.
Efficiency on large datasets	Slower	Faster
Implementation	Simple and straightforward	Slightly more complex due to divide-and-conquer logic
When to use	When data is unsorted or the list is small	When data is sorted and the list is large
Requires sorted data?	No	Yes

Big-O describes how fast an algorithm grows with input size by providing an upper bound (i.e., the maximum time or steps) the algorithm might take.

Understanding the \(log_2(n)\) Steps in Binary Search

In binary search, you start with \(n\) elements, and in each step, you divide the array into 2 halves. Each halving step cuts the size by half:

**Binary Search Halving Process**
Step	Remaining Elements
Start	n
Step 1	n/2
Step 2	n/4
Step 3	n/8
...	...
Step k	n/(2^k)

We keep halving until only 1 element is left: \( \frac{n}{2^k} = 1\)

Solve for k (number of steps): \( \frac{n}{2^k} = 1 \Rightarrow n = 2^k \)

Take log base 2 on both sides: \( log_2(n) = k \)

So: \( k = log_2(n) \)

♣ The number of times you can divide n by 2 before you reach 1 element is \( log_2(n) = k \).
♣ That’s why binary search takes \( log_2(n) = k \) steps in the worst case.

Lower Bound for Searching

Theorem: On the Lower Bound for Searching
Any algorithm that solves the search problem for an n-element list by comparing the target element x to the list items must do at least ⌞\(log_2n\)⌟+1 comparisons in the worst case.

This theorem gives us a lower bound on the number of comparisons required in the worst case for any algorithm that uses comparisons to solve the search problem. Since binary search does no more work than this required minimum amount, binary search is an optimal algorithm in its worst-case behavior.

(Lower bound means no algorithm can get faster than this no matter what, so if an algorithm actually does this, then it is optimal for worst case scenario)
Note:
(1) ⌞⌟ means floor. The floor is the largest integer that is smaller than or equal to the number inside the floor signs.
For example:
⌞2.9⌟=2
⌞2.2⌟=2
⌞2⌟=2

(2) log is actually base 2 even though they didn't put the base in the statement of the theorem.It is stated elsewhere.

(3) \(log_2x = y\) means \(2^y=x\) so logn means that we want the exponent we would need to put on 2 in order to get n.

(4) Example 1:
Any algorithm that solves the search problem for a 5687-element list by comparing the target element x to the list items must do at least __________ comparisons in the worst case.
Solution: ⌞\(log_2 5687\) ⌟+1 = ⌞12.????⌟ + 1 = 12 + 1 = 13

How did we get this? The table below has powers of 2 up to \(2^{13}\), and if we want to know the value of x when \(2^x=5687\) (because log 5687 = x means \(2^x=5687\)), then looking in the table (4096 < 5687 < 8192), so x must be between 12 and 13. Because of the floor, ⌞12.???⌟ = 12, we don't have to know the value of the ????.

x	\(2^x\)
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192

(5) Example 2:
Any algorithm that solves the search problem for a 52-element list by comparing the target element x to the list items must do at least __________ comparisons in the worst case.
Solution: ⌞\(log_2 52\) ⌟+1 = ⌞5.????⌟ + 1 = 5 + 1 = 6

(6) Example 3:
Any algorithm that solves the search problem for a 654-element list by comparing the target element x to the list items must do at least __________ comparisons in the worst case.
Solution: ⌞ \(log_2 654\) ⌟+1 = ⌞9.????⌟ + 1 = 9 + 1 = 10

Reference

saylor academy