Chapter 7: Graph Algorithms

Section 7.4 Traversal Algorithms

In this section we deal with a simpler problem--we only want to write down all the nodes of a simple, connected graph G in some orderly way. This means we must find a path that visits each node at least once, but we can visit it more than once if we don't write it down again. We can also retrace arcs on the graph if necessary, and clearly this would in general be necessary if we were to visit each node in a tree. This process is called graph traversal . We already have several mechanisms for tree traversal (Section 6.2). The two algorithms in this section generalize traversal to apply to any simple, connected graph.

Breadth-First Search

• ☆ BFS is a graph traversal algorithm that explores all neighbors at the current level before moving to the next level.
• ☆ It starts at a selected node, visits all directly connected neighbors, and uses a queue to track the next level of nodes to explore.
• ☆ BFS can be implemented using a queue.

In breadth-first search, beginning at an arbitrary node a, we first fan out from node a to visit nodes that are adjacent to a; then we fan out from those nodes, and so on, almost like the concentric circles of ripples in a pond. Figure 7.15 shows the first few nodes visited in the same graph as Figure 7.13, this time using breadth-first search.

To write the breadth-first search algorithm in an elegant fashion, we will use a queue structure. A queue is simply a line in which new arrivals are added at the back and departures take place at the front

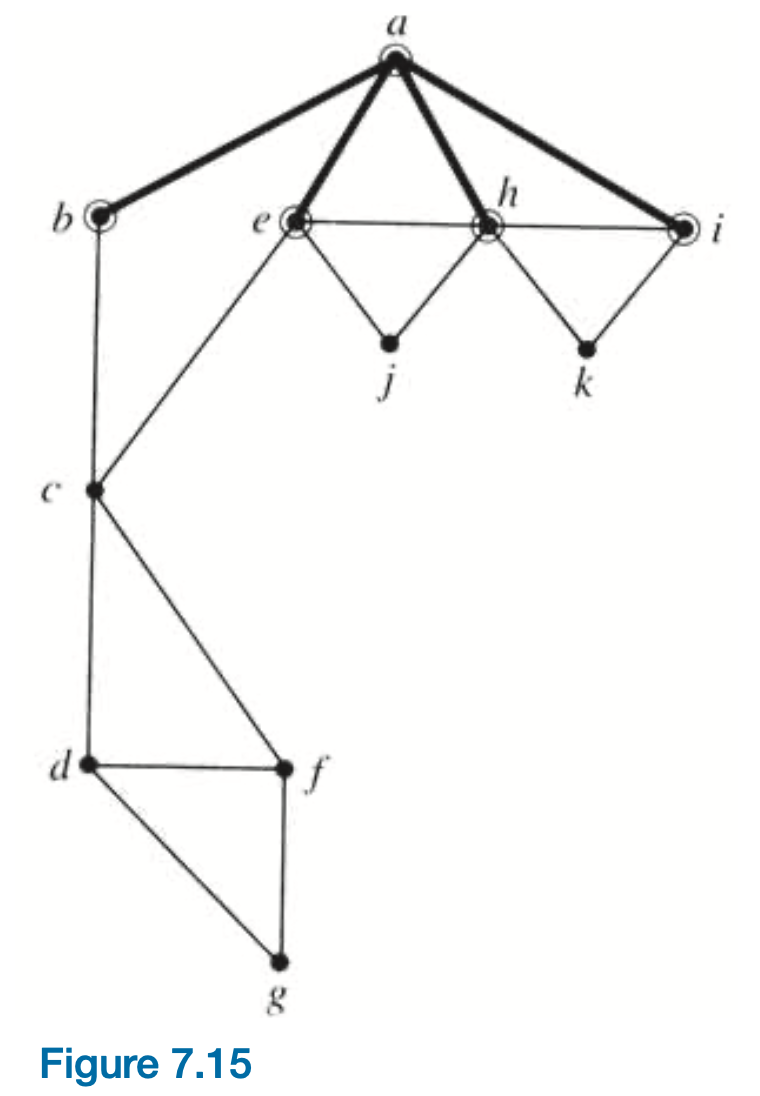
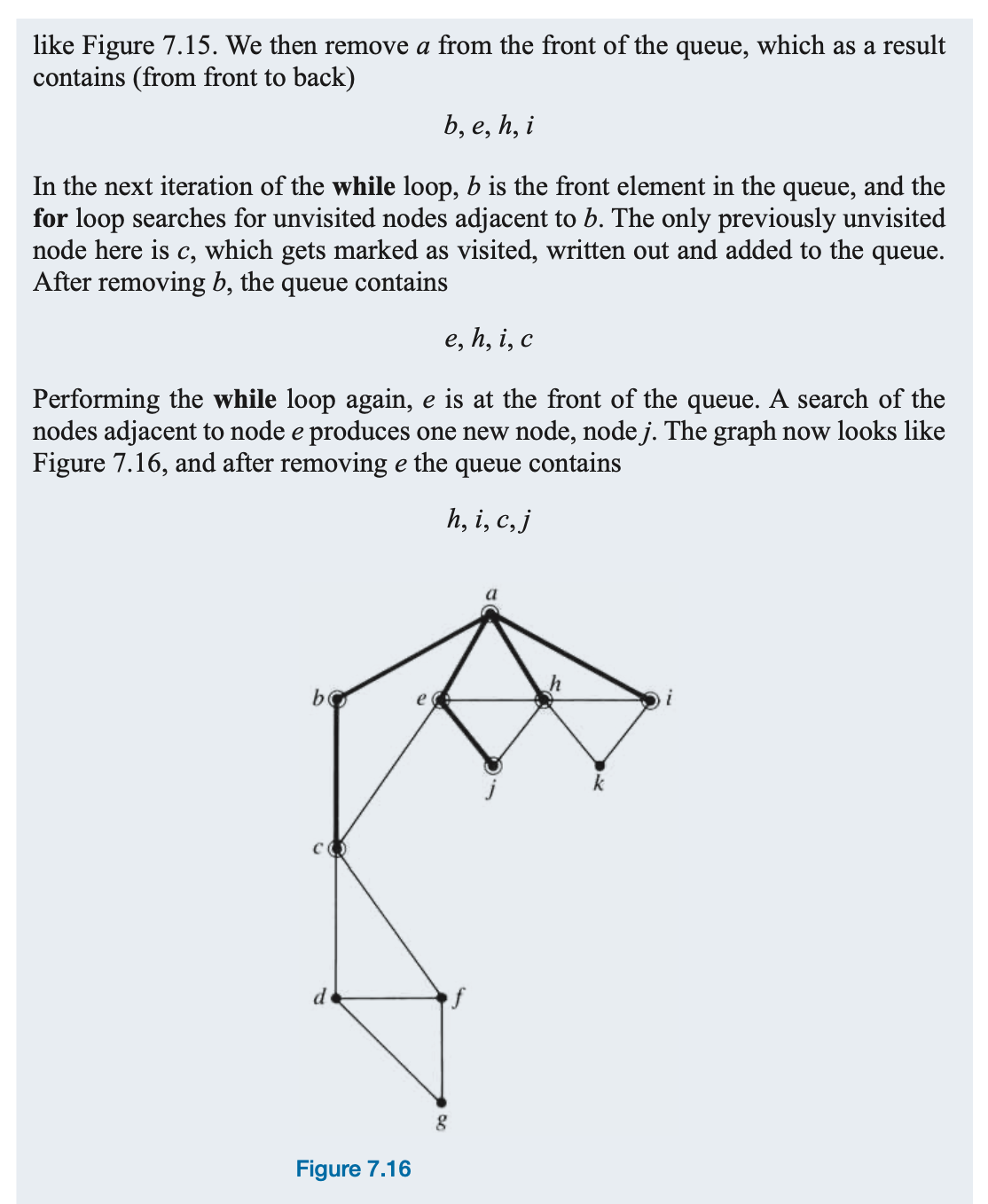
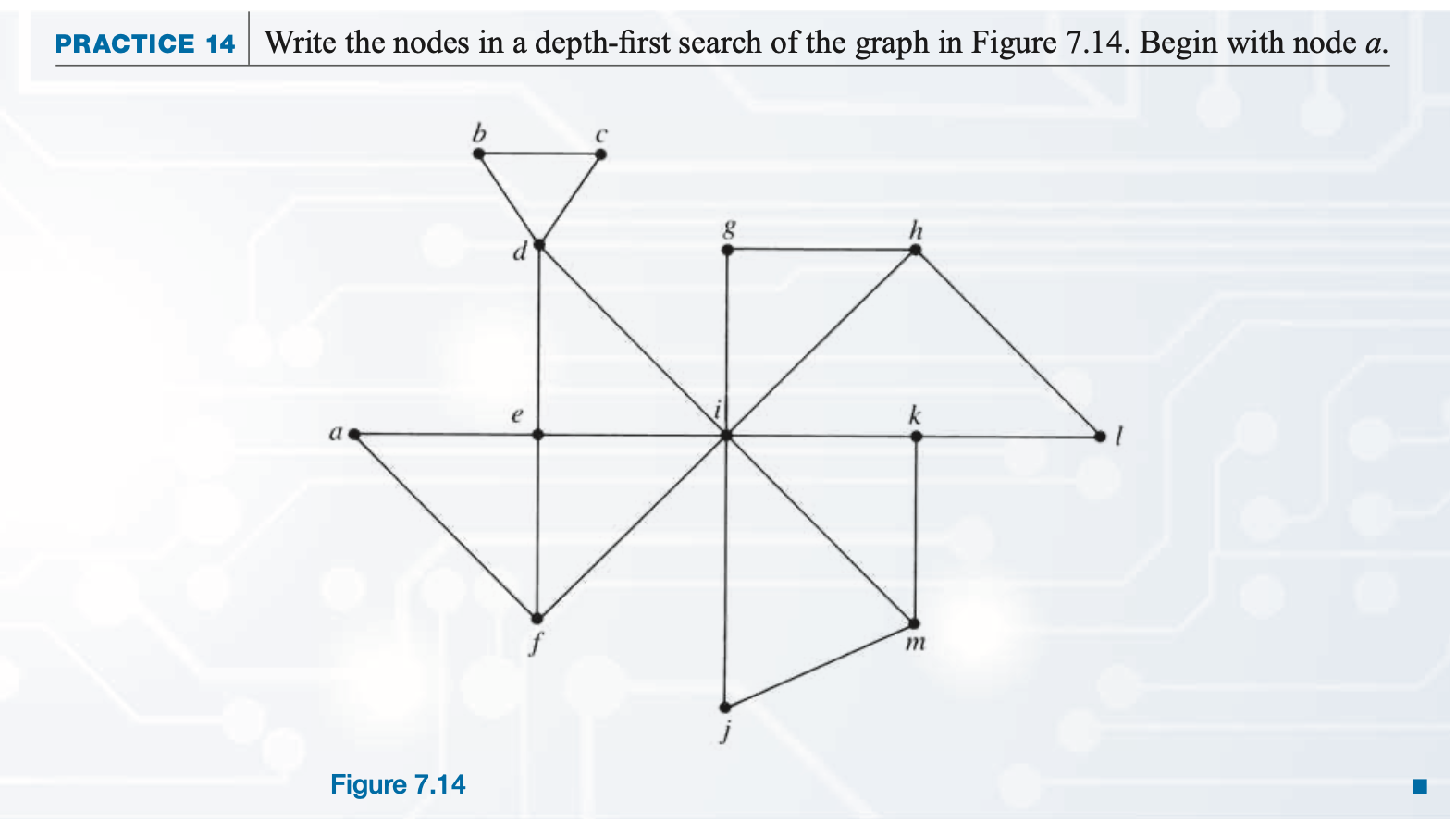
Practice

Please write the nodes in a breadth-first search of the graph in Figure 7.14.

BFS Shortest Path for Unweighted Grid (JavaScript version)

BFS Shortest Path Demo

Reference

saylor academy