Chapter 7: Graph Algorithms
Section 7.1 Directed Graphs and Binary Relations
In this section we confine our attention to (unweighted) directed graphs with no parallel arcs. Because there are no parallel arcs in the graph, the adjacency matrix will be a Boolean matrix, that is, a matrix whose only elements are 0s and 1s. Conversely, given an \(n \times n\) Boolean matrix, we can reconstruct the directed graph that the matrix represents, and it will have no parallel arcs. Thus there is a one-to-one correspondence, which we can picture as
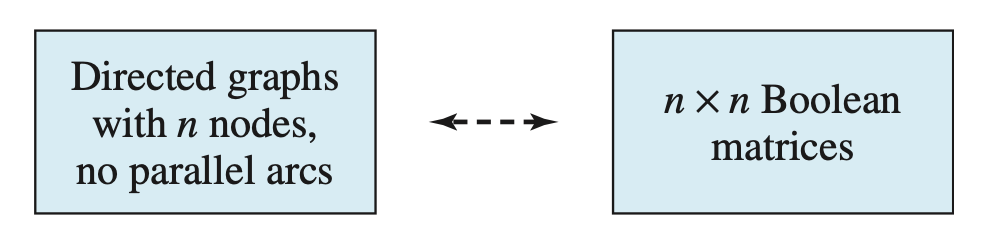
Directed Graphs and Binary Relations
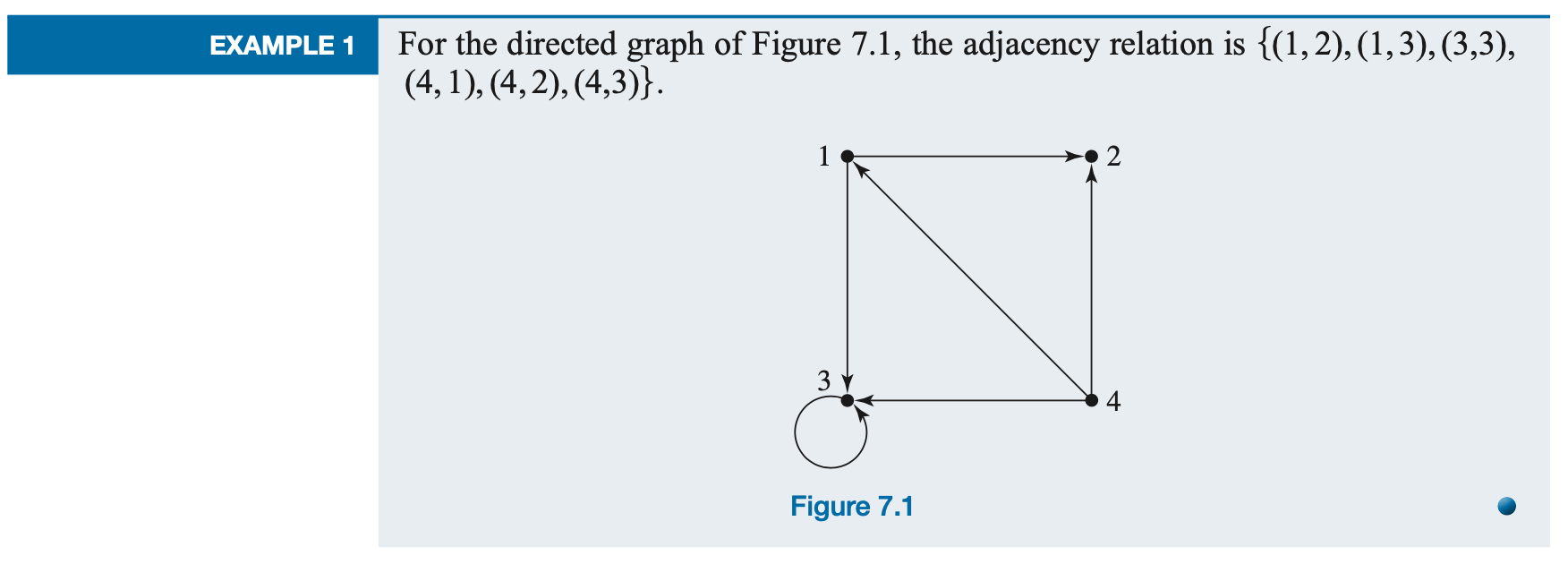
Suppose G is a directed graph with n nodes and no parallel arcs. Let N be the set of nodes. If \( (n_i, n_j) \) is an ordered pair of nodes, then there either is or is not an arc in G from \(n_i\) to \(n_j\). We can use this property to define a binary relation on the set N:This relation is the adjacency relation of the graph.
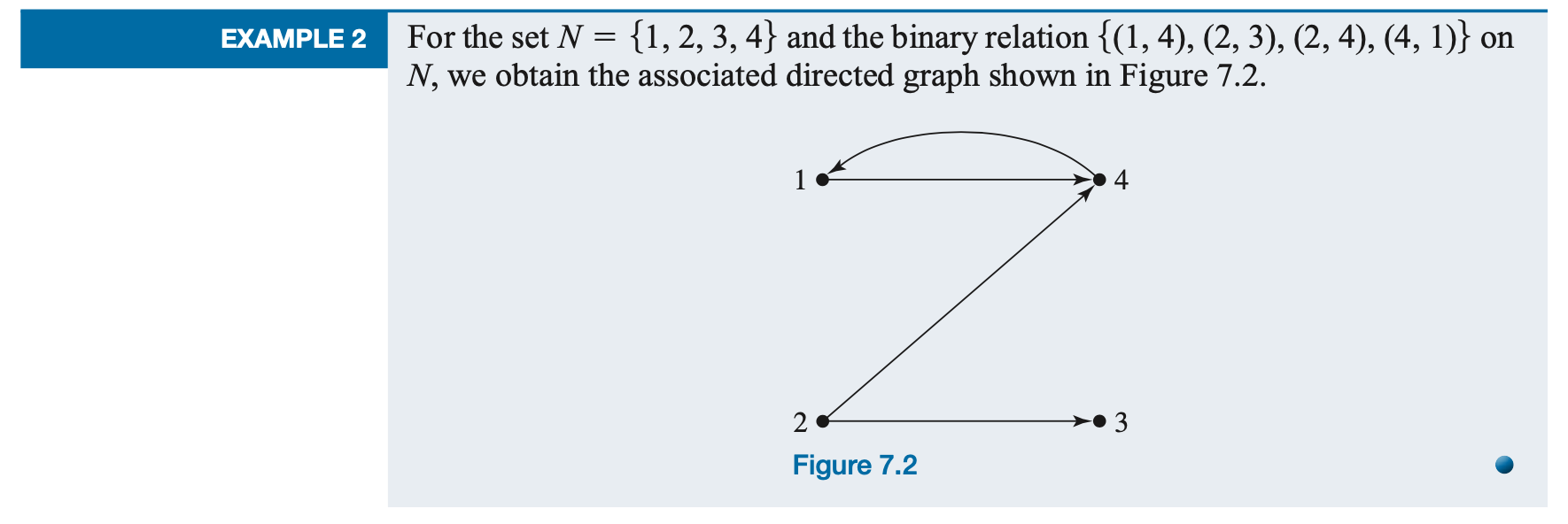
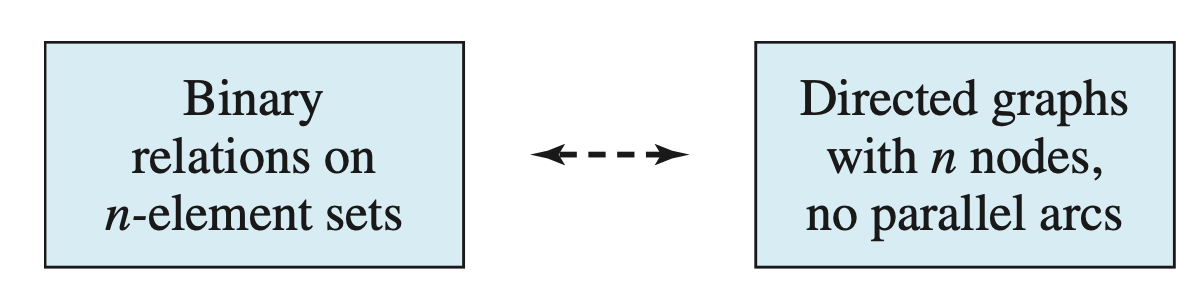
Conversely, if ρ is a binary relation on a set N, we can define a directed graph G with N as the set of nodes, and an arc from \(n_i\) to \(n_j\) if and only if \(n_i\) ρ \(n_j\). G will have no parallel arcs.
We now have another one-to-one correspondence:
Thus We have three equivalent sets:

An item from any of the three sets has corresponding representations in the other two sets.
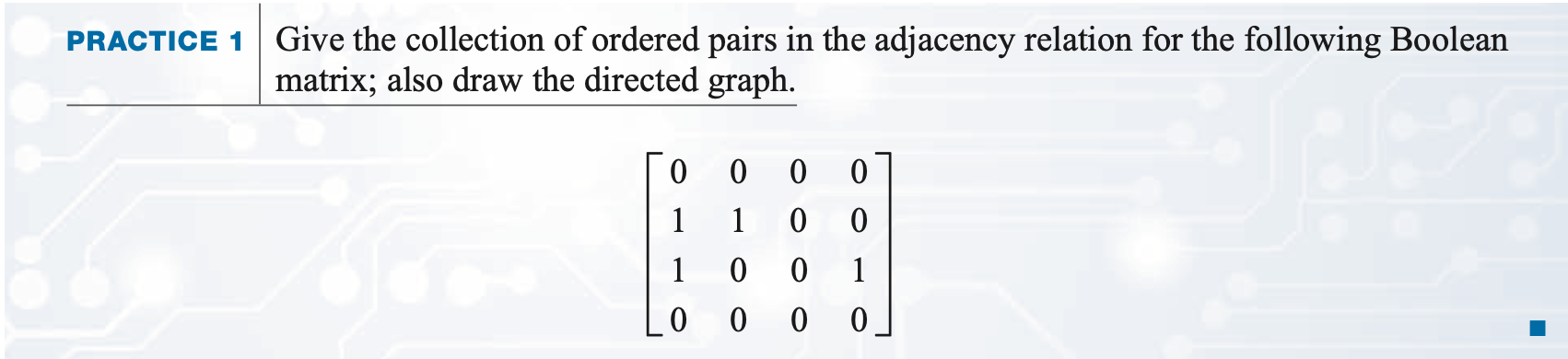
Practice 1
Reachability
Reachable Node:In a directed graph, node \(n_j\) is reachable from node \(n_i\) if there is a path from \(n_i\) to \(n_j\).

The adjacency matrix a of a directed graph G with n nodes and no parallel arcs will have a 1 in position i, j if there is an arc from \(n_i\) to \(n_j\). This would be a path of length 1 from \(n_i\) to \(n_j\). The adjacency matrix by itself therefore tells us about a limited form of reachability, via length-1 paths. However, let us perform the Boolean matrix multiplication \(A \times A\) . We'll denote this product by \(A^{(2)}\) to distinguish it from \(A^2\), the result of \(A·A\) using ordinary matrix multiplication. A path of length 2 from \(n_i\) to \(n_j\) will exist if and only there is a path of length 2 passing through at least one of the nodes from 1 to n, that is, if and only if \(A^{(2)}[i,j] = 1\). Therefore the entries in \(A^{(2)}\) tell us about reachability via length-2 paths. This pattern continues, with \(A^{(n)}\) indicating reachability via length-n paths. Basic reachability only requires paths of up to \(n\) nodes, as longer paths simply add cycles without changing the reachability.
Practice 2
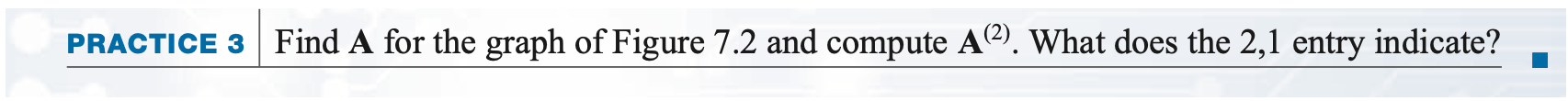
The matrix \(A^{(2)}\) indicates the presence or absence of length-2 paths. We might surmise that this result holds for arbitrary powers and path lengths.

We can define a reachability matrix R by:
Then \(n_j\) is reachable from \(n_i\) is and only if entry \(i,j\) in R is positive.
To summarize, corresponding to the three equivalent representations of adjacency relation ρ, directed graph G, and adjacency matrix A, we have
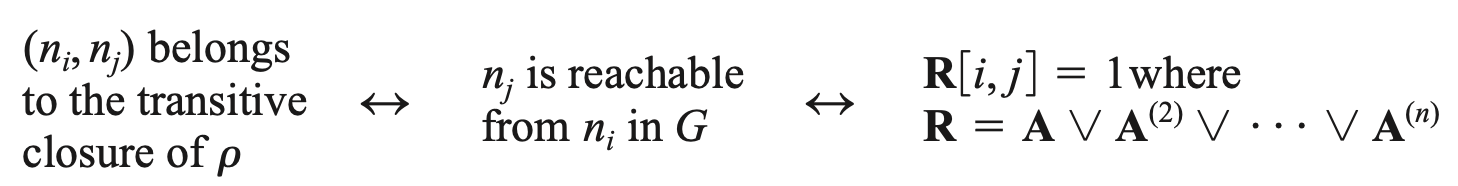
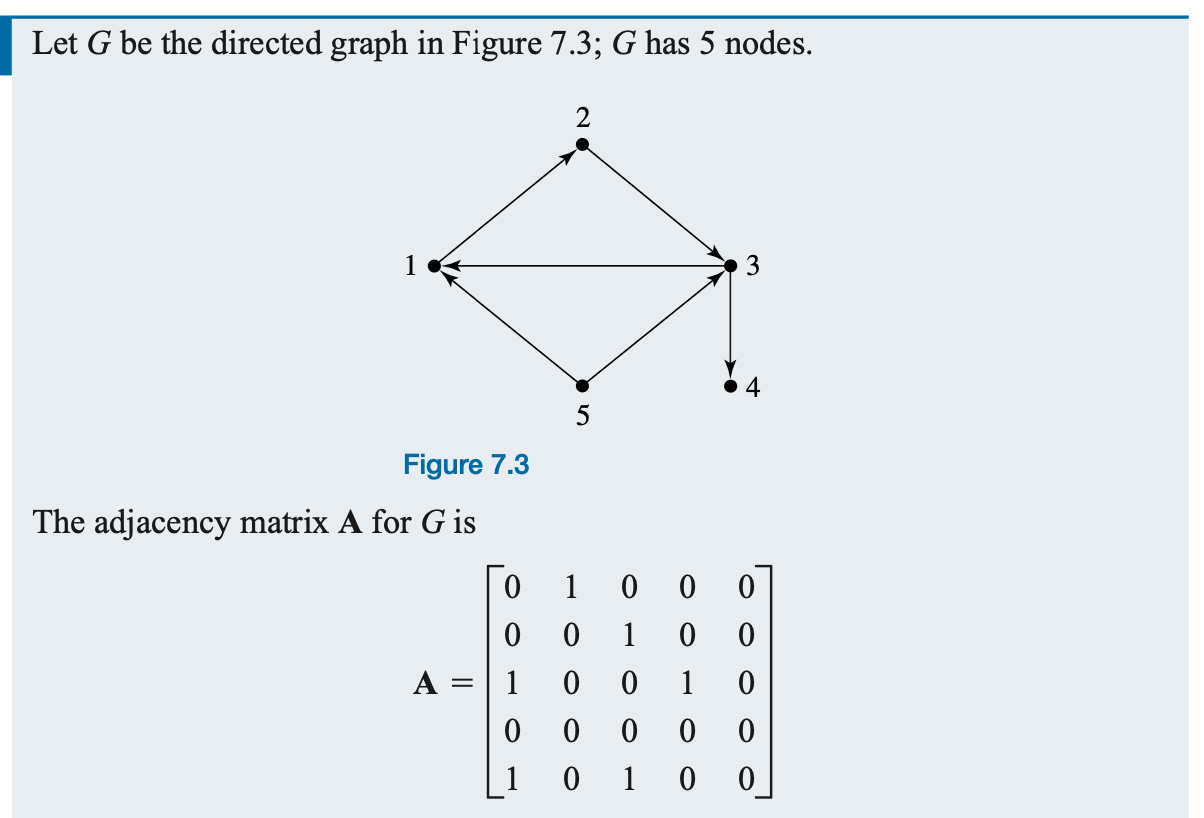
Example


Practice
Please compute reachability matrix R for the directed graph of Figure 7.2. What information does column 2 convey?\(R = A ∨ A^{(2)} ∨ A^{(3)} ∨ A^{(4)}\)
