Chapter X: Binary Encoding Scheme

Section X.1 Weighted Codes

Binary Encoding

Although the binary number system has many practical advantages and is widely used in digital computers, in many cases it is convenient to work with the decimal number system, especially when the communication between man and the machine is extensive since most numerical data generated by man are in terms of decimal numbers. To simplify the communication problem between man and machine, a number of codes have been devised so that the decimal digits are represented by sequences of binary digits.

Classification of binary codes

• Weighted Codes

• *Binary to Decimal
• *BCD Code
• *Self-Complementing Code
• *Two's complement

• Non-Weighted Codes

• *Excess-3 Code
• *Gray Code

• Alphanumeric Codes

• *American Standard Code for Information Interchange (ASCII)
• *Extended Binary Coded Decimal Interchange Code (EBCDIC)

• Error Detecting Codes

• *Parity Bit

• Error Correcting Codes

• *7-Bit Hamming Code

Weighted Codes

Weighted binary codes are those binary codes that obey the positional weight principle. Each position of the number represents a specific weight.

The weighted code is characterized by assigning a specific weight to each binary digit (bit). The decimal value represented by the code is equal to the sum of each bit's weight multiplied by the binary digit (1 or 0) at that position. This sum corresponds directly to the decimal digit being represented.

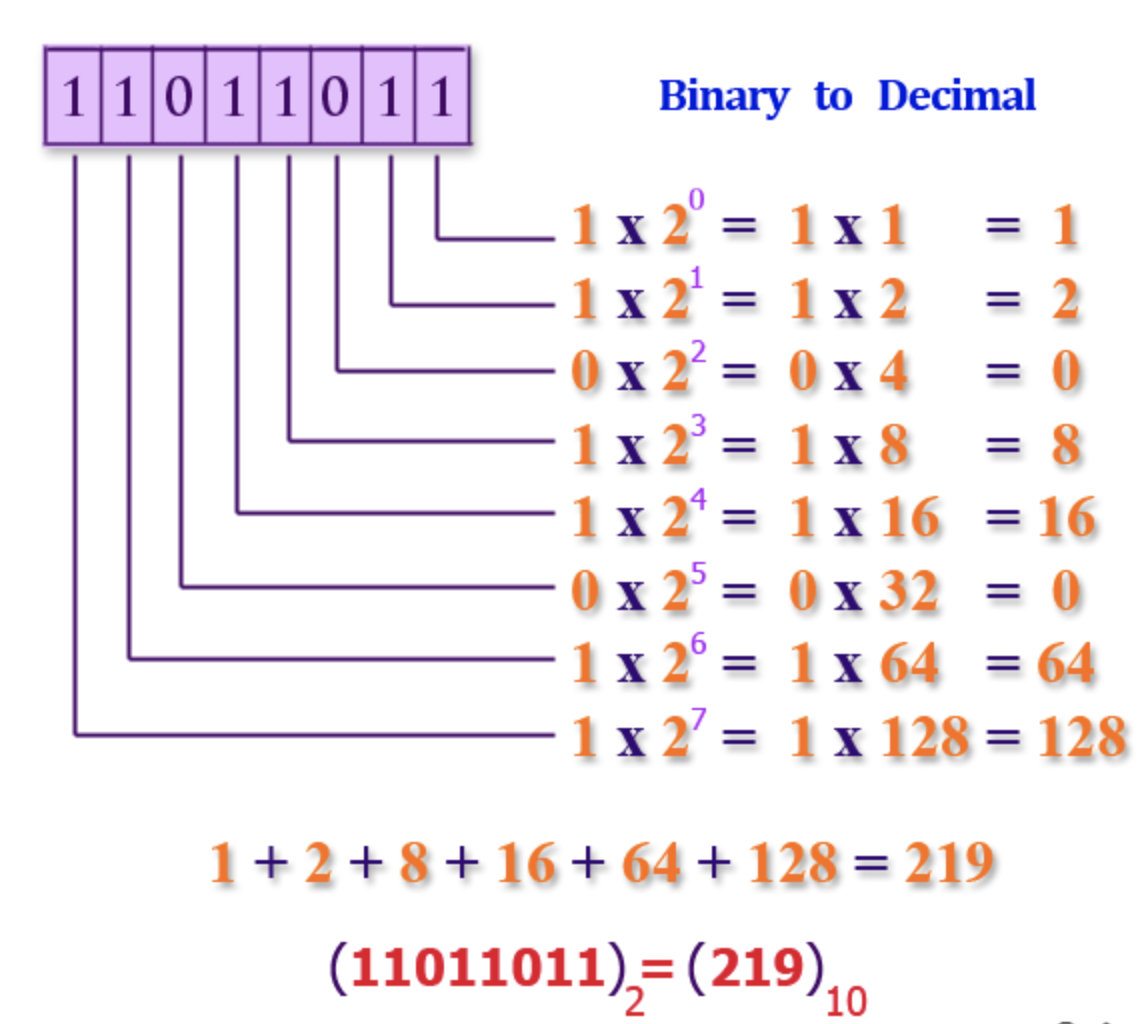
Binary to Decimal

---

If \( w_1, w_2, w_3, w_4, w_5, w_6, w_7,\) and \(w_8\) are the weights of the binary digits and \(x_1, x_2, x_3, x_4, x_5, x_6, x_7 \) and \(x_8\) are the corresponding digit values, then the decimal digit \(D = w_8 \times x_8 + w_7 \times x_7 + w_6 \times x_6 + w_5 \times x_5 + w_4 \times x_4 + w_3 \times x_3 + w_2 \times x_2 + w_1 \times x_1 \) is represented by the binary sequence \(x_8x_7x_6x_5x_4x_3x_2x_1\). A sequence of binary digits which represents a decimal digit is called a code word. Thus the above sequence \(x_8x_7x_6x_5x_4x_3x_2x_1\) is the code word for \(D\).

The binary digits in the following code are assigned the weights 128, 64, 32, 16, 8, 4, 2, 1. As a result of this weight assignment, the code word that corresponds to each decimal digit is the binary equivalence of that digit, so 219 is represented by 11011011.

Binary to Decimal Table (0-15)

---

Hexadecimal (base 16)	Decimal (base 10)	Binary (base 2)
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
A	10	1010
B	11	1011
C	12	1100
D	13	1101
E	14	1110
F	15	1111

Hexadecimal, often abbreviated as hex, is a base-16 numeral system. It uses 16 symbols to represent numbers:

• The digits 0 to 9 represent values 0 to 9.
• The letters A to F represent values 10 to 15.

Hexadecimal is widely used in computer systems because it is more compact and human-readable than binary (base-2):

• One hexadecimal digit represents 4 binary bits (a nibble).
• For example:

				Binary: 1111 1111
				Hexadecimal: FF
			

Example Conversions:

• 1. Binary to Hexadecimal:

			Binary 110101101011 --> Group into nibbles: 1101 0110 1011 --> Hex: D6B
			

• 2. Decimal to Hexadecimal:

			Let’s convert the decimal number 756 to hexadecimal.
			1. 756 ÷ 16 = 47 remainder 4
				Record 4 (this will be the last digit of the hex number).
			2. 47 ÷ 16 = 2 remainder 15
				Record 15. Since 15 in hexadecimal is F, we write F.
			3. 2 ÷ 16 = 0 remainder 2
				Record 2 (this is the last step as the quotient is now 0).
			4. Read from Bottom to Top:
				The hexadecimal number for decimal 756 is 2F4.
			

Hexadecimal is extensively used in programming, memory addressing, and color codes in web design (e.g., #FF5733).

BCD(binary-coded-decimal) Code

---

To represent the 10 decimal digits (0, 1, ..., 9) in binary, at least 4 binary digits (bits) are required.

If \( w_1, w_2, w_3,\) and \(w_4\) are the weights of the binary digits and \(x_1, x_2, x_3, \) and \(x_4\) are the corresponding digit values, then the decimal digit \(D = w_4 \times x_4 + w_3 \times x_3 + w_2 \times x_2 + w_1 \times x_1 \) is represented by the binary sequence \(x_4x_3x_2x_1\). A sequence of binary digits which represents a decimal digit is called a code word. Thus the above sequence \(x_4x_3x_2x_1\) is the code word for \(D\).

The binary digits in the first code in the following table are assigned the weights 8, 4, 2, 1. As a result of this weight assignment, the code word that corresponds to each decimal digit is the binary equivalence of that digit; e.g., 5 is represented by 0101, and so on. This code is known as the BCD (binary-coded-decimal) code. This scheme can also be referred to as Simple Binary-Coded Decimal (SBCD) or BCD 8421. In this code each decimal digit is represented by a 4-bit binary number. BCD is a way to express each of the decimal digits with a binary code. In the BCD, with four bits we can represent sixteen numbers (0000 to 1111). But in BCD code only first ten of these are used (0000 to 1001). The remaining six code combinations i.e. 1010 to 1111 are invalid in BCD. For each of the codes in the table, the decimal digit that corresponds to a given code word is equal to the sum of the weights in those binary positions which are 1s.

BCD Application

A binary clock might use LEDs to express binary values.

Self-Complementing Code

---

A self-complementing code is one where flipping each bit in the binary code of a digit gives the binary code of its 9’s complement.

In a self-complementing code, the binary representation of a decimal digit D (such as 0 through 9) has a special property: if you invert (flip) each bit of that code, you get the binary representation of \(9-D\) ( which is known as the "9's complement" of D).

A necessary condition for a code to be self-complementing is that the sum of the weights must equal 9.

Example: 2 4 2 1 Self-Complementing Code

Decimal Digit	2 4 2 1 Code	Flipped Code	Decimal of Flipped Code	9−D
0	0000	1111	\(2\times1+4\times1+2\times1+1\times1 = 9\)	\(9 = 9-0\)
1	0001	1110	\(2\times1+4\times1+2\times1+1\times0 = 8\)	\(8 = 9-1\)
2	0010	1101	\(2\times1+4\times1+2\times0+1\times1 = 7\)	\(7 = 9-2\)
3	0011	1100	\(2\times1+4\times1+2\times0+1\times0 = 6\)	\(6 = 9-3\)
4	0100	1011	\(2\times1+4\times0+2\times1+1\times1 = 5\)	\(5 = 9-4\)
5	1011	0100	\(2\times0+4\times1+2\times0+1\times0 = 4\)	\(4 = 9-5\)
6	1100	0011	\(2\times0+4\times0+2\times1+1\times1 = 3\)	\(3 = 9-6\)
7	1101	0010	\(2\times0+4\times0+2\times1+1\times0 = 2\)	\(2 = 9-7\)
8	1110	0001	\(2\times0+4\times0+2\times0+1\times1 = 1\)	\(1 = 9-8\)
9	1111	0000	\(2\times0+4\times0+2\times0+1\times0 = 0\)	\(0 = 9-9\)

Example: 6 4 2 -3 Self-Complementing Code

Decimal Digit	6 4 2 -3 Code	Flipped Code	Decimal of Flipped Code	9−D
0	0000	1111	\(6\times1+4\times1+2\times1-3\times1 = 9\)	\(9 = 9-0\)
1	0101	1010	\(6\times1+4\times0+2\times1-3\times0 = 8\)	\(8 = 9-1\)
2	0010	1101	\(6\times1+4\times1+2\times0-3\times1 = 7\)	\(7 = 9-2\)
3	1001	0110	\(6\times0+4\times1+2\times1-3\times0 = 6\)	\(6 = 9-3\)
4	0100	1011	\(6\times1+4\times0+2\times1-3\times1 = 5\)	\(5 = 9-4\)
5	1011	0100	\(6\times0+4\times1+2\times0-3\times0 = 4\)	\(4 = 9-5\)
6	0110	1001	\(6\times1+4\times0+2\times0-3\times1 = 3\)	\(3 = 9-6\)
7	1101	0010	\(6\times0+4\times0+2\times1-3\times0 = 2\)	\(2 = 9-7\)
8	1010	0101	\(6\times0+4\times1+2\times0-3\times1 = 1\)	\(1 = 9-8\)
9	1111	0000	\(6\times0+4\times0+2\times0-3\times0 = 0\)	\(0 = 9-9\)

It is apparent that the representations of some decimal numbers in the (2,4,2,1) and (6,4,2,-3) codes are not unique. For example, in the (2,4,2,1) code, decimal 7 may be represented by 1101 as well as by 0111.

There exist only four positively weighted self-complementing codes, name, (2,4,2,1), (3,3,2,1), (4,3,1,1), (5,2,1,1).
In addition, there exist 13 self-complementing codes with positive and negative weights.

Why This Is Useful

• You can find the 9's complement of any digit by simply flipping the bits in its code.
• This makes arithmetic operations, especially subtraction, easier to implement in digital circuits, as no extra calculations are needed to find complements.

Two's complement:

---

Two's complement is a mathematical technique and a binary number representation used in computing to represent signed integers—that is, both positive and negative whole numbers. It is the most common method for encoding negative numbers in binary form within computers and digital systems.

Example: Convert a Negative Decimal Number -5 to a 4-bit binary number:

• 1.Find the Binary Representation of the Positive Number: 5 in binary (using 4 bits) is: 0101
• 2.Find the One's Complement: Flip all the bits: 1010
• 3.Add 1 to the One's Complement: 1010+1=1011
• 4.Result: The binary representation of -5 in 4 bits is 1011

Example: Converting a Binary Number 1011 in Two's Complement to Decimal Number:

• 1.Identify the Sign Bit
• If the left Most Significant Bit (MSB) is 0, the number is positive or zero.
• If the left Most Significant Bit (MSB) is 1, the number is negative.
• 2.Find the One's Complement: Flip all the bits: 0100
• 3.Add 1 to the One's Complement: 0100+1=0101
• 4.Convert the Result to Decimal: \(0*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 5\)
• 5.Apply Negative Sign: -5

Value Ranges:

• Positive Numbers: 0 \( \sim 2^{n-1}-1\)
• Negative Numbers: \(-2^{n-1} \sim \) \(-1\)

Practice Examples:

(1) Convert a Negative Decimal Number −18 to an 8-bit binary number using Two's Complement.

(2) Converting a Binary Number 1011 0101 in Two's Complement to a Decimal Number.

Reference

BCD Code
Binary Codes
Gray to Binary and Binary to Gray conversion
Gray Code